Grawitacyjna energia potencjalna – zadanie nr 1

Oblicz grawitacyjną energię potencjalną układu dwóch cząstek przedstawionych na poniższym rysunku. Następnie wyobraź sobie, że odległość R  wzrosła czterokrotnie. Ile wynosi wartość pracy W  wykonanej przez siłę grawitacji działającej pomiędzy cząstkami?

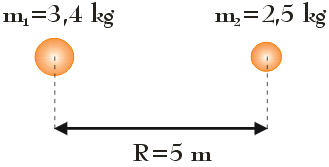
Grawitacyjna energia potencjalna układu dwóch ciał wyraża się następująco:

$$E_p = \hspace{.1cm} – \hspace{.05cm} G \hspace{.05cm} \frac{m \hspace{.05cm} M}{r}$$

gdzie:
G  – stała grawitacji równa 6,67 ⋅ 10^-11 N ⋅ m²/kg²,
m  i M  to masa jednego i drugiego ciała,
r  – odległość pomiędzy środkami ciał.

W naszym przypadku mamy do czynienia z dwiema cząstkami o masach m₁  i m₂, oddalonych od siebie o R, dlatego też powyższe wyrażenie możemy zapisać jako:

$$E_p = \hspace{.1cm} – \hspace{.05cm} G \hspace{.05cm} \frac{m_1 \hspace{.05cm} m_2}{R}$$

Masa obydwu cząstek, jak i odległość R  podane są w treści zadania, zatem grawitacyjna energia potencjalna dla tego układu cząstek wynosi:

$$E_p = \hspace{.1cm} – \hspace{.1cm} 6,\hspace{-.1cm}67 \cdot 10^{-11} \tfrac{\textrm{N} \hspace{.05cm} \cdot \hspace{.05cm} \textrm{m}^2}{\textrm{kg}^2} \cdot \frac{3,\hspace{-.1cm}4 \hspace{.05cm} \textrm{kg} \cdot 2,\hspace{-.1cm}5 \hspace{.05cm} \textrm{kg}}{5 \hspace{.05cm} \textrm{m}} = \hspace{.1cm} – \hspace{.1cm} 11,\hspace{-.1cm}3 \cdot 10^{-11} \hspace{.05cm} \textrm{J}$$

Zajmijmy się teraz drugą częścią zadania. Gdy odległość R  pomiędzy cząstkami wzrośnie czterokrotnie, wartość grawitacyjnej energii potencjalnej E_p  zmaleje cztery razy. Jak możesz przeczytać w artykule Grawitacyjna energia potencjalna, zmiana grawitacyjnej energii potencjalnej ΔE_p  równa się pracy W  wykonanej przez siłę ciężkości, wziętej z przeciwnym znakiem:

$$\hspace{.1cm} – \hspace{.1cm} W = \Delta \hspace{.03cm} E_p = E_{p,konc} \hspace{.1cm} – \hspace{.1cm} E_{p,pocz}$$

gdzie:
E_p,konc  – grawitacyjna energia potencjalna układu po czterokrotnym zwiększeniu odległości R pomiędzy cząstkami,
E_p,pocz  – grawitacyjna energia potencjalna układu w sytuacji początkowej, czyli przed zwiększeniem odległości R.

Grawitacyjną energię potencjalną układu cząstek dla sytuacji przed oraz po zwiększeniu odległości R możemy przedstawić jako:

$$E_{p,pocz} = \hspace{.1cm} – \hspace{.05cm} G \hspace{.05cm} \frac{m_1 \hspace{.05cm} m_2}{R}$$

$$E_{p,konc} = \hspace{.1cm} – \hspace{.05cm} G \hspace{.05cm} \frac{m_1 \hspace{.05cm} m_2}{4 \hspace{.05cm} R}$$

Po podstawieniu powyższych zależności do wzoru na ΔE_p , otrzymamy:

$$\hspace{.1cm} – \hspace{.1cm} W = E_{p,konc} \hspace{.1cm} – \hspace{.1cm} E_{p,pocz} = \hspace{.1cm} – \hspace{.05cm} G \hspace{.05cm} \frac{m_1 \hspace{.05cm} m_2}{4 \hspace{.05cm} R} \hspace{.1cm} – \hspace{.1cm} \left( \hspace{.1cm} – \hspace{.1cm} G \hspace{.05cm} \frac{m_1 \hspace{.05cm} m_2}{R} \right) = \frac{3}{4} \hspace{.05cm} G \hspace{.05cm} \frac{m_1 \hspace{.05cm} m_2}{R}$$

Po odwróceniu znaków, podstawieniu wartości liczbowych oraz wykonaniu obliczeń, uzyskamy wartość pracy W  równą:

$$W = \hspace{.1cm} – \hspace{.1cm} \frac{3}{4} \hspace{.05cm} G \hspace{.05cm} \frac{m_1 \hspace{.05cm} m_2}{R} = \hspace{.1cm} – \hspace{.1cm} \frac{3}{4} \cdot 6,\hspace{-.1cm}67 \cdot 10^{-11} \tfrac{\textrm{N} \hspace{.05cm} \cdot \hspace{.05cm} \textrm{m}^2}{\textrm{kg}^2} \cdot \frac{3,\hspace{-.1cm}4 \hspace{.05cm} \textrm{kg} \cdot 2,\hspace{-.1cm}5 \hspace{.05cm} \textrm{kg}}{5 \hspace{.05cm} \textrm{m}} = \hspace{.1cm} – \hspace{.1cm} 8,\hspace{-.1cm}5 \cdot 10^{-11} \hspace{.05cm} \textrm{J}$$