Grawitacyjna energia potencjalna

Na każde ciało o masie m wyrzucone ku górze z powierzchni Ziemi (czy też z każdego innego ciała niebieskiego) z prędkością początkową V₀ , działa siła ciężkości (grawitacji), zwrócona w kierunku Ziemi. Efektem działania tej siły jest stopniowe zmniejszanie się energii kinetycznej E_k  ciała, aż do chwili, w której wartość E_k  stanie się równa zero. Z zupełnie odwrotną sytuacją mamy do czynienia podczas swobodnego spadku ciała, kiedy to wartość energii E_k ciała zaczyna stopniowo wzrastać, osiągając maksimum tuż przed upadkiem ciała na Ziemię. W obydwu wspomnianych przypadkach zmiany energii kinetycznej ΔE_k  ciała związane są z pracą wykonywaną nad ciałem przez siłę ciężkości, której wartość podczas wznoszenia się ciała jest ujemna (W < 0), z kolei podczas swobodnego spadku – dodatnia (W > 0). Każdorazowa zmiana wartości energii kinetycznej ciała, spowodowana działaniem siły ciężkości, powoduje zmianę grawitacyjnej energii potencjalnej układu ciało – Ziemia, której to obecnie poświęcimy nieco więcej uwagi.

Grawitacyjna energia potencjalna – wzór

Ogólnie rzecz biorąc grawitacyjna energia potencjalna E_p  związana jest z odległością r  pomiędzy ciałami. Gdybyśmy chcieli obliczyć wartość energii potencjalnej układu dwóch ciał (np. układu kamień – Ziemia) skorzystalibyśmy z poniższego wzoru (wyprowadzenie poniższej zależności znajdziesz w artykule Grawitacyjna energia potencjalna – wyprowadzenie wzoru):

$$E_p = \hspace{.1cm} – \hspace{.05cm} G \hspace{.05cm} \frac{m \hspace{.05cm} M}{r}$$

gdzie:
G – stała grawitacji równa 6,67 ∙ 10^-11 N ∙ m²/kg²,
m , M – masa jednego i drugiego ciała,
r – odległość między środkami ciał.

Znak minus w powyższym wzorze oznacza, że zmiana energii potencjalnej ΔE_p  układu ciał jest przeciwna do pracy W  wykonanej przez siłę ciężkości (ΔE_p  = – W). Zauważ, że gdy r → ∞, wartość E_p  dąży do zera, z kolei, gdy r  przyjmuje skończoną wartość, E_p  jest ujemne.

Musisz pamiętać, że grawitacyjna energia potencjalna E_p  odnosi się zawsze do układu ciał traktowanego jako całość a nie do każdego ciała z osobna. Wyjątkiem od tej reguły jest każdy przypadek, w którym masa m  jednego z ciał jest dużo większa od masy M  pozostałego (pozostałych) ciał (m  ≫ M). Najprostszym przykładem takiego układu jest układ kamień – Ziemia, dla którego (gdy tylko kamień porusza się w pobliżu Ziemi) zmiany energii potencjalnej są praktycznie całkowicie związane ze zmianą energii kinetycznej kamienia, ponieważ zmiana energii kinetycznej Ziemi jest praktycznie niemierzalna. W takim przypadku zamiast mówić o grawitacyjnej energii potencjalnej układu kamień – Ziemia możemy mówić o grawitacyjnej energii potencjalnej kamienia.

Grawitacyjna energia potencjalna układu czterech ciał

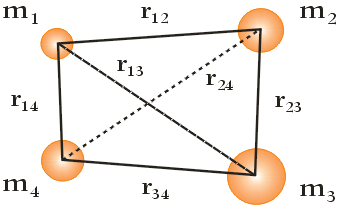
Wzór na E_p , podany wyżej, jest słuszny tylko i wyłącznie dla układu składającego się z dwóch ciał. W przypadku, gdy układ składa się z większej ilości ciał, każdą parę ciał należy rozważać niezależnie od siebie (pomijając wpływ innych ciał), obliczając dla niej grawitacyjną energię potencjalną E_p  i następnie poszczególne wartości energii pododawać do siebie. Dla układu ciał przedstawionego na powyższym rysunku wartość E_p  wynosi:

$$E_p = \hspace{.1cm} – \hspace{.05cm} G \hspace{.05cm} \left( \frac{m_1 \hspace{.05cm} m_2}{r_{12}} + \frac{m_1 \hspace{.05cm} m_3}{r_{13}} + \frac{m_1 \hspace{.05cm} m_4}{r_{14}} + \frac{m_2 \hspace{.05cm} m_3}{r_{23}} + \frac{m_2 \hspace{.05cm} m_4}{r_{24}} + \frac{m_3 \hspace{.05cm} m_4}{r_{34}} \right)$$

Należy zaznaczyć, że wartość zmiany grawitacyjnej energii potencjalnej ΔE_p  nie zależy od drogi przebytej przez dowolne ciało (np. podczas wznoszenia, czy opadania), ponieważ siła grawitacji działająca na takie ciało jest siłą zachowawczą.