Prawa Keplera
Od bardzo dawna ruch planet zachodzący na tle nieba fascynował badaczy na całym świecie. Pomimo wielu odkryć poczynionych na przestrzeni wieków, ruch planet pozostawał jedną wielką zagadką. Sytuacja ta uległa nagłej zmianie, kiedy niemiecki matematyk i astronom Johannes Kepler (1571 – 1630) sformułował na początku siedemnastego wieku trzy empiryczne prawa opisujące ruch planet, które obecnie, na jego cześć, noszą nazwę praw Keplera. Do sformułowania tychże praw przyczynił się obszerny zbiór danych obserwacyjnych zebranych przez duńskiego astronoma Tycho Brahe (1546 – 1601) – nauczyciela Keplera.
Pierwsze prawo Keplera
Na poniższym rysunku przedstawiono planetę o masie m poruszającą się wokół Słońca (o masie M ) po orbicie w kształcie elipsy. W jednym z dwóch ognisk tej elipsy, oznaczonych literami K i K’, znajduje się Słońce. Każde ognisko znajduje się w odległości ea od środka elipsy, gdzie e oznacza mimośród orbity, z kolei a – półoś wielką orbity, czyli połowę większej osi elipsy. Mimośród orbity to wielkość charakteryzująca kształt orbity: e = 0 odpowiada orbicie kołowej – szczególnemu przypadkowi orbity eliptycznej, w której ogniska elipsy znajdują się w tym samym punkcie, e = 1 – orbicie eliptycznej. Wartości e oraz a determinują wielkość orbity, po której wokół Słońca poruszają się planety.
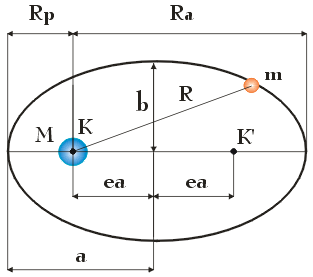
Na rysunku literą b zaznaczono również półoś małą orbity, czyli połowę mniejszej osi elipsy oraz peryhelium Rp i aphelium Ra, czyli punkt orbity, w którym odległość planety od Słońca jest, odpowiednio, najmniejsza oraz największa.
W poniższej tabeli przedstawiono wartość mimośrodu e, półosi wielkiej orbity a oraz obwód orbity dla każdej z planet Układu Słonecznego:
| Planeta | Mimośród e (-) | Półoś wielka orbity a (j.a.) | Obwód orbity (j.a.) |
|---|---|---|---|
| Merkury | 0,20563 | 0,38709 | 2,406 |
| Wenus | 0,00671 | 0,72333 | 4,545 |
| Ziemia | 0,01671 | 1,00000 | 6,179 |
| Mars | 0,09341 | 1,52366 | 9,553 |
| Jowisz | 0,04839 | 5,20336 | 31,912 |
| Saturn | 0,05415 | 9,53707 | 59,879 |
| Uran | 0,04717 | 19,19126 | 120,515 |
| Neptun | 0,00859 | 30,06896 | 30,44 |
1 j.a. = 149 597 870 691 m – jedna jednostka astronomiczna odpowiada średniej odległości Ziemi od Słońca.
Drugie prawo Keplera
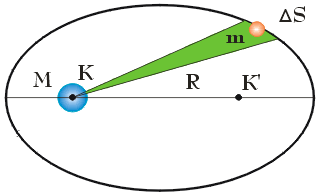
Drugie prawo Keplera jest równoważne zasadzie zachowania momentu pędu. Można wykazać, że szybkość zmiany pola powierzchni ΔS , zakreślanego przez linię łączącą planetę ze Słońcem (zobacz rysunek poniżej) wynosi:
$$\frac{dS}{dt} = \tfrac{1}{2} \hspace{.05cm} r^2 \hspace{.05cm} \omega$$
gdzie:
r – odległość dzieląca Słońce od planety,
ω – prędkość kątowa obrotu linii łączącej Słońce z planetą.
Oznaczając przez L moment pędu planety względem Słońca:
$$L = m \hspace{.05cm} r^2 \hspace{.05cm} \omega$$
dostaniemy, że:
$$\frac{dS}{dt} = \frac{L}{2 \hspace{.05cm} m}$$
Zgodnie z drugim prawem Keplera pochodna dS /dt jest stała, a więc stała musi być także wartość momentu pędu L. Oznacza to, że planeta znajdująca się daleko od powierzchni Słońca (np. w aphelium) porusza się po orbicie wolniej, niż wtedy, gdy znajduje się blisko Słońca (np. w peryhelium).
Trzecie prawo Keplera
Treść trzeciego prawa Keplera opisuje poniższy wzór:
$$T^2 = \frac{4 \hspace{.05cm} \pi^2}{G M} \hspace{.05cm} a^3$$
gdzie:
M – masa ciała wokół którego krąży planeta (w naszym przypadku M to masa Słońca),
a – półoś wielka orbity eliptycznej.
Powyższe wyrażenie obowiązuje również w przypadku orbit kołowych, dla których w miejsce a należy wstawić promień r takiej orbity. Wyprowadzenie tego wzoru znajdziesz tutaj: Trzecie prawo Keplera – wyprowadzenie wzoru.
Z trzeciego prawa Keplera wynika, że stosunek $\dfrac{T^2}{a^3}$ powinien być stały dla wszystkich orbit związanych z planetami krążącymi wokół tego samego ciała o masie M. Dla planet wchodzących w skład naszego Układu Słonecznego stosunek ten, bliski wartości 3, jest w przybliżeniu stały, potwierdzając tym samym słuszność tego prawa.

1 komentarz
Marta
Dodano dnia 19 listopada 2013 o godz. 18:12
Super strona! Wielkie dzięki 🙂