Grawitacyjna energia potencjalna – wyprowadzenie wzoru

Wyprowadzenie wzoru:

Wyobraźmy sobie sytuację, w której piłkę o masie m  wyrzucamy z powierzchni Ziemi w kierunku pionowym w górę, po torze przedstawionym na poniższym rysunku. Interesuje nas znalezienie wyrażenia na grawitacyjną energię potencjalną E_p  układu piłka – Ziemia w punkcie K, znajdującym się w odległości r  od środka Ziemi.

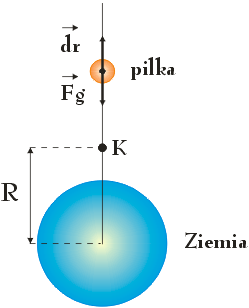
Obliczmy na początek pracę W  wykonaną nad piłką przez siłę grawitacji $\vec{F}_g$  przy przemieszczeniu piłki od punktu K  do punktu leżącego w nieskończonej odległości od środka Ziemi:

$$W = \int\limits_{r}^{\infty} \vec{F}_g(r) \hspace{.1cm} \vec{dr} = \int\limits_{r}^{\infty} F_g(r) \hspace{.1cm} dr \hspace{.1cm} \textrm{cos} \hspace{.05cm} \alpha$$

gdzie:
F_g ( r )  – siła grawitacji,
dr  – różniczkowe (bardzo niewielkie) przemieszczenie piłki wzdłuż toru, po którym się porusza,
α  – kąt zawarty pomiędzy wektorem $\vec{F}_g(r)$  a  $\vec{dr}$, który zgodnie z rysunkiem wynosi 180^o.

W powyższym wzorze, aby rozpisać wyrażenie $\vec{F}_g (r) \hspace{.1cm} \vec{dr}$ skorzystaliśmy ze wzoru na iloczyn skalarny dwóch wektorów. Podstawiając następnie w miejsce F_g ( r )  wyrażenie na siłę grawitacji oraz korzystając z faktu, że cos 180^o = -1, dostaniemy:

$$W = \hspace{.1cm} – \hspace{.1cm} \int\limits_{r}^{\infty} G \hspace{.05cm} \frac{m \hspace{.05cm} M}{r^2} \hspace{.05cm} dr = \left[ G \hspace{.05cm} \frac{m \hspace{.05cm} M}{r} \right]_r^\infty = \left[ 0 \hspace{.15cm} – \hspace{.05cm} G \hspace{.05cm} \frac{m \hspace{.05cm} M}{r} \right] = \hspace{.1cm} – \hspace{.1cm} G \hspace{.05cm} \frac{m \hspace{.05cm} M}{r}$$

gdzie:
m  – masa piłki,
M  – masa Ziemi.

W  (jak napisaliśmy wcześniej) jest pracą potrzebną do przeniesienia piłki z punktu K  do nieskończoności. Aby znaleźć wyrażenie na grawitacyjną energię potencjalną E_p  w punkcie K  skorzystamy z poniższego wyrażenia, w którym pracę W  przedstawimy jako zmianę energii potencjalnej ΔE_p  (zobacz: Grawitacyjna energia potencjalna):

$$\Delta \hspace{.03cm} E_p = E_{p,konc} \hspace{.1cm} – \hspace{.1cm} E_{p,pocz} = \hspace{.1cm} – \hspace{.1cm} W$$

gdzie:
E_p,konc  – grawitacyjna energia potencjalna w nieskończoności,
E_p,pocz  – grawitacyjna energia potencjalna w punkcie K.

Ponieważ energia potencjalna dowolnego ciała w nieskończonej odległości od Ziemi jest równa zero – E_p,konc  = 0 – zatem:

$$E_{p,pocz} = E_p = W = \hspace{.1cm} – \hspace{.1cm} G \hspace{.05cm} \frac{m \hspace{.05cm} M}{r}$$