Grawitacja w pobliżu Ziemi – zadanie nr 3

Jednorodna kula ma masę M  = 3000 kg i promień R  = 3 m. Ile wynosi wartość siły grawitacji, jaką kula ta działa na cząstkę o masie m  = 5 kg umieszczoną w odległości r  równej a) 5 m oraz b) 1 m od środka kuli? Podaj zależność wartości siły grawitacji od wartości r,  gdy r  < R.

W zadaniu możemy wyróżnić dwa przypadki: jeden, w którym cząstka o masie m  znajduje się na zewnątrz kuli o promieniu R  (r  > R ) oraz drugi, w którym cząstka znajduje się wewnątrz tej kuli (r  < R ). Dla obu tych przypadków mamy obliczyć siłę grawitacji F  działającą na cząstkę ze strony kuli. Wartość tej siły obliczymy korzystając z poniższego równania (odległość cząstki od kuli jest bardzo niewielka, dlatego też, aby skorzystać z tego wyrażenia stosujemy twierdzenie o powłoce):

$$F = G \hspace{.05cm} \frac{m \hspace{.05cm} M}{r^2}$$

gdzie:
G  – stała grawitacji równa 6,67 ⋅ 10^-11 N ⋅ m²/kg²,
m  – masa cząstki,
M  – masa kuli,
r  – odległość cząstki od środka kuli.

Pierwszy przypadek: r  > R

Zajmijmy się teraz pierwszym przypadkiem, dla którego r  > R. Cząstka znajduje się na zewnątrz kuli, a więc kula oddziałuje na cząstkę całą swoją masą równą M. W związku z tym wartość siły grawitacji F₁, wynosi:

$$F_1 = G \hspace{.05cm} \frac{m \hspace{.05cm} M}{r^2} = 6,\hspace{-.1cm}67 \cdot 10^{-11} \hspace{.05cm} \tfrac{\textrm{N} \hspace{.05cm} \cdot \hspace{.05cm} \textrm{m}^2}{\textrm{kg}^2} \cdot \frac{5 \hspace{.05cm} \textrm{kg} \cdot 3000 \hspace{.05cm} \textrm{kg}}{\left( 5 \hspace{.05cm} \textrm{m} \right)^2} = 4 \cdot 10^{-8} \hspace{.05cm} \textrm{N} = 40 \hspace{.05cm} \textrm{nN}$$

Drugi przypadek: r  < R

W drugim przypadku cząstka znajduje się wewnątrz kuli (r  < R ), co oznacza, że tylko pewna jej część zawarta w obszarze nie przekraczającym promienia r  (czyli odległości dzielącej cząstkę od środka kuli) będzie oddziaływać na cząstkę. Pozostała część kuli nie będzie wywierać żadnego wpływu na wartość siły grawitacji, ponieważ wypadkowa sił grawitacyjnych działających na cząstkę ze strony tej części kuli będzie po prostu równa zero (zobacz: Grawitacja wewnątrz Ziemi). Masa kuli M’  zawarta w obszarze ograniczonym promieniem r  nie jest podana w treści zadania. Możemy ją jednak z łatwością wyznaczyć, ponieważ wiemy, że kula ta jest jednorodna tzn. gęstość kuli jest stała w całej jej objętości. Korzystając z tego faktu możemy zapisać gęstość ρ_w  tej części kuli jako:

$$\rho_w = \frac{M’}{\tfrac{4}{3} \hspace{.05cm} \pi \hspace{.05cm} r^3}$$

Całkowita gęstość kuli ρ_c  wynosi zatem:

$$\rho_c = \frac{M}{\tfrac{4}{3} \hspace{.05cm} \pi \hspace{.05cm} R^3}$$

Porównując stronami powyższe wyrażenia, dostaniemy:

$$\frac{M’}{\tfrac{4}{3} \hspace{.05cm} \pi \hspace{.05cm} r^3} = \frac{M}{\tfrac{4}{3} \hspace{.05cm} \pi \hspace{.05cm} R^3} \hspace{1cm} \longrightarrow \hspace{1cm} M’ = M \hspace{.05cm} \frac{r^3}{R^3}$$

Znając wartość masy M’  możemy przystąpić do obliczenia siły grawitacji F₂ :

$$F_2 = G \hspace{.05cm} \frac{m \hspace{.05cm} M’}{r^2} = G \hspace{.05cm} \frac{m \cdot M \cdot r^3}{r^2 \cdot R^3} = G \hspace{.05cm} \frac{m \hspace{.05cm} M}{R^3} r$$

Po podstawieniu do powyższego wyrażenia wartości liczbowych oraz wykonaniu obliczeń, otrzymamy:

$$F_2 = 6,\hspace{-.1cm}67 \cdot 10^{-11} \hspace{.05cm} \tfrac{\textrm{N} \hspace{.05cm} \cdot\hspace{.05cm} \textrm{m}^2}{\textrm{kg}^2} \cdot \frac{5 \hspace{.05cm} \textrm{kg} \cdot 3000 \hspace{.05cm} \textrm{kg}}{\left( 3 \hspace{.05cm} \textrm{m} \right)^3} \cdot 1 \hspace{.05cm} \textrm{m} = 3,\hspace{-.1cm}7 \cdot 10^{-8} \hspace{.05cm} \textrm{N} = 37 \hspace{.05cm} \textrm{nN}$$

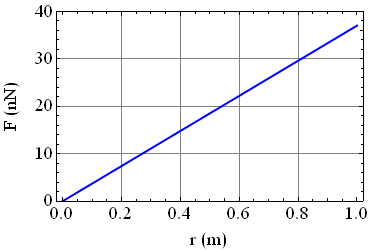
Wzór $F_2 = G \hspace{.05cm} \frac{m \hspace{.05cm} M}{R^3} r$  opisuje zależność siły grawitacji F  w funkcji odległości r, gdy r  < R. Zauważ, że siła F  maleje (wzrasta) liniowo, gdy r  maleje (wzrasta). Dla lepszego zobrazowania tej sytuacji zależność F(r)  została schematycznie przedstawiona na poniższym rysunku (r  = 0 m odpowiada środkowi kuli, r  = 1 m – odległości w jakiej znajduje się cząstka wewnątrz kuli):