Energia w ujęciu mechaniki relatywistycznej
Albert Einstein w sformułowanej przez siebie w roku 1905 szczególnej teorii względności oprócz wykazania, że przestrzeń i czas są ze sobą wzajemnie powiązane, dowiódł także, że masę dowolnego obiektu należy traktować jako jedną z postaci energii. Oznacza to, że masa i energia (podobnie jak czas i przestrzeń) są ze sobą ściśle powiązane i nie mogą być rozpatrywane niezależnie od siebie.
Masa a energia
Przed opublikowaniem przez Einsteina szczególnej teorii względności masa i energia były rozważane, zwłaszcza przez chemików, jako dwie niezależne od siebie wielkości. Dlaczego? Ponieważ podczas zachodzenia reakcji chemicznych, a więc procesów oddziaływania atomów i cząsteczek, przemianie na inne formy energii ulega tylko niewielka (niemierzalna) część masy. Nie dziwi więc fakt, że do początku XX wieku nie istniał żaden związek pomiędzy tymi wielkościami. Sytuacja ta zmieniła się wraz z nastaniem ery fizyki jądrowej, która potwierdziła teorię sformułowaną przez Einsteina i stała się przepustką do odkrycia wielu zjawisk fizycznych zachodzących w mikroświecie. W przypadku reakcji jądrowych, tj. procesów związanych z oddziaływaniem jąder atomowych i cząstek elementarnych, zmianę masy można z łatwością wyznaczyć m.in. dlatego, że energia uwalniana w trakcie tych procesów może być nawet kilka milionów razy większa w porównaniu z energią uwalnianą podczas reakcji chemicznych. Od tego czasu uwzględnianie w reakcjach jądrowych przemian związanych z masą i energią stało się rutynowym postępowaniem i nikogo nie dziwi już fakt, że te dwie wielkości fizyczne są ze sobą wzajemnie powiązane.
Energia spoczynkowa E0
Relację wiążącą masę oraz energię opisuje poniższe równanie, które (bez indeksu 0) jest najprawdopodobniej najbardziej znanym równaniem fizyki:
$$E_0 = m \hspace{.05cm} c^2$$
gdzie E0 to energia spoczynkowa związana z masą dowolnego obiektu. Zgodnie z teorią Einsteina, ciało posiada energię nawet wtedy, gdy spoczywa i jest to tylko i wyłącznie konsekwencją faktu, że ciało posiada określoną masę. W poniższej tabeli podane są wartości energii spoczynkowych wybranych obiektów m.in. elektronu, protonu oraz neutronu, a więc cząstek stanowiących budulec atomów.
| Obiekt | Masa (kg) | E0 (J) | E0 (MeV) |
|---|---|---|---|
| Elektron | 9,1031 ⋅ 10-31 | 8,18 ⋅ 10-14 | 0,511 |
| Proton | 1,6726 ⋅ 10-27 | 1,50 ⋅ 10-10 | 938,31 |
| Neutron | 1,6749 ⋅ 10-27 | 1,51 ⋅ 10-10 | 939,59 |
| Atom węgla | 19,9378 ⋅ 10-27 | 1,79 ⋅ 10-9 | 11,18 ⋅ 103 |
| Ołówek | 3 ⋅ 10-2 | 2,69 ⋅ 1015 | 1,68 ⋅ 1028 |
| Człowiek | 70 | 6,29 ⋅ 1018 | 3,93 ⋅ 1031 |
| Słoń | 5500 | 4,94 ⋅ 1020 | 3,09 ⋅ 1033 |
Zauważ, że energia spoczynkowa elektronu, czy protonu jest bardzo mała w porównaniu z innymi obiektami przedstawionymi w tabeli, dlatego też zwłaszcza w fizyce jądrowej i fizyce cząstek elementarnych bardzo rzadko wyraża się ją w dżulach (a masę w kg). Zazwyczaj masę obiektu wyraża się w atomowych jednostkach masy (ozn. a.j.m. lub u):
$$1 \hspace{.05cm} \textrm{a. j. m.} = 1,\hspace{-.1cm}66 \cdot 10^{-27} \hspace{.05cm} \textrm{kg}$$
a energię w elektronowoltach (ozn. eV):
$$1 \hspace{.05cm} \textrm{eV} = 1,\hspace{-.1cm}60 \cdot 10^{-19} \hspace{.05cm} \textrm{J}$$
Wartość energii spoczynkowej, jak stwierdziliśmy powyżej, nie zależy od tego czy ciało spoczywa, czy też porusza się z pewną prędkością. Jednakże w przypadku, gdy ciało jest w ruchu, posiada oczywiście dodatkową energię – energię kinetyczną. Przy założeniu, że energia potencjalna jest równa zero, całkowita energia takiego ciała wyniesie:
$$E = E_0 + E_k$$
Energia całkowita
Energię całkowitą ciała wyraża się także poniższym wzorem:
$$E = \gamma \hspace{.05cm} m \hspace{.05cm} c^2$$
gdzie γ to oczywiście współczynnik Lorentza.
Korzystając z powyższych relacji z łatwością otrzymamy wyrażenie na energię kinetyczną ciała w ujęciu mechaniki relatywistycznej, słuszne dla wszystkich fizycznie dozwolonych prędkości:
$$E_k = E \hspace{.1cm} – \hspace{.1cm} E_0 = E \hspace{.1cm} – \hspace{.1cm} m \hspace{.05cm} c^2 = m \hspace{.05cm} c^2 \left( \gamma \hspace{.1cm} – \hspace{.1cm} 1 \right)$$
Na poniższym wykresie przedstawiono zależność energii kinetycznej elektronu od parametru β (β = V /c ) dla przypadku klasycznego (nierelatywistycznego) oraz relatywistycznego.
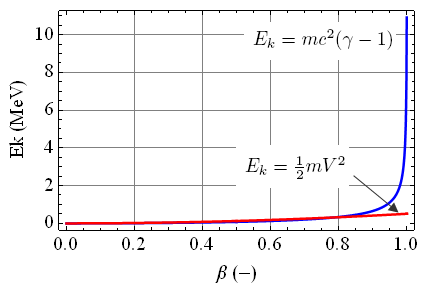
Kiedy stosować wzory relatywistyczne?
Zauważ, że w zakresie małych prędkości (mniejszych od prędkości światła c ) obydwie krzywe pokrywają się, tak więc w tym obszarze możemy (oprócz wzoru relatywistycznego) korzystać także, z dobrym przybliżeniem, ze wzoru klasycznego. W przypadku prędkości bliskich c obydwie krzywe rozbiegają się: krzywa czerwona reprezentująca ujęcie klasyczne wzrasta powoli, podczas gdy krzywa niebieska (relatywistyczna) pnie się gwałtownie do góry, dążąc do nieskończoności. Oznacza to, że w obszarze bardzo dużych prędkości musimy korzystać tylko i wyłącznie ze wzoru relatywistycznego.
Z powyższego wykresu otrzymujemy także bardzo cenną informację dotyczącą pracy jaką należy wykonać, aby zwiększyć prędkość cząstki np. o kilka procent. W zakresie małych prędkości wartość pracy (równa różnicy energii kinetycznych) jest niewielka (krzywe ulegają tylko nieznacznemu wzrostowi). Zupełnie z inną sytuacją mamy do czynienia w obszarze prędkości bliskich c – w tym przypadku praca jaką należy wykonać może przyjmować bardzo dużą wartość, rosnąć aż do nieskończoności. Wykonanie pracy o nieskończonej wartości jest oczywiście niemożliwym do wykonania, potwierdzając tym samym jedno z założeń szczególnej teorii względności Einsteina głoszące, że obiekty obdarzone masą nie mogą osiągnąć prędkości światła.

Dodaj komentarz