Współczynnik Lorentza

Bardzo często przeglądając różne materiały dotyczące fizyki relatywistycznej możesz spotkać się z wyrażeniami, w których występuje mała grecka litera gamma – γ. Wielkość ta nazywana współczynnikiem Lorentza – nazwana tak na cześć holenderskiego fizyka H.A. Lorentza (1853 – 1928) – spełnia bardzo istotną rolę w fizyce. Za chwilę przekonasz się jaką.

Wzory opisujące dylatację czasu czy skrócenie długości można w oparciu o współczynnik Lorentza γ, zdefiniowany jako

$$\gamma = \frac{1}{\sqrt{1 \hspace{.15cm} – \hspace{.05cm} \left( \tfrac{V}{c} \right)^2}} = \frac{1}{\sqrt{1 \hspace{.15cm} – \hspace{.05cm} \beta ^2 }}$$

zapisać w bardziej uproszczonej formie:

$$\Delta \hspace{.05cm} t = \gamma \hspace{.1cm} \Delta \hspace{.05cm} t_0 \hspace{1cm} , \hspace{1cm} S = \frac{S_0}{\gamma}$$

Zależność między γ a β

Bezwymiarowy stosunek prędkości $\frac{V}{c}$ , oznaczony małą grecką literą β, jest traktowany jako prędkość w jednostkach c  (c  jak z pewnością pamiętasz jest prędkością światła w próżni). Zgodnie z postulatem stałej prędkości światła wartość parametru β dla ciał obdarzonych masą jest zawsze mniejsza od jedności (prędkość ciał posiadających masę jest zawsze mniejsza od c ), w związku z czym γ jest zawsze większe niż 1 (pod warunkiem, że V  będzie różne od zera). Tą sytuację przedstawia poniższy rysunek:

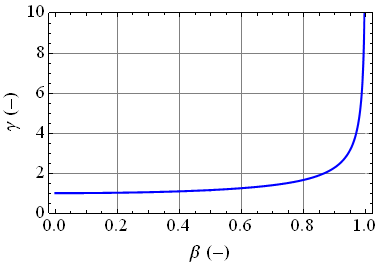
Okazuje się, że dla prędkości $V \lt 0,\hspace{-.1cm}1 \hspace{.1cm} c$  (a więc $\beta \lt 0,\hspace{-.1cm}1$) wartość γ nie odbiega znacząco od jedności, w związku z czym opis zachodzących zdarzeń może opierać się na wzorach fizyki nierelatywistycznej. Wraz ze wzrostem wartości parametru β wartość współczynnika Lorentza zaczyna stopniowo wzrastać. Gdy β jest bliskie jedności, tj. prędkość obiektu staje się bliska prędkości światła, γ zaczyna gwałtownie rosnąć a wraz z nią wzrasta także odstępstwo wyników między wzorami mechaniki nierelatywistycznej a relatywistycznej.