Względność czasu

Zgodnie ze szczególną teorią względności Einsteina przestrzeń i czas są ze sobą wzajemnie powiązane, co oznacza, że odstęp czasu pomiędzy zdarzeniami jest uzależniony od odległości dzielącej je w przestrzeni (i na odwrót). Zależność ta, pomiędzy czasem a przestrzenią, jest różna dla obserwatorów poruszających się względem siebie, co wykażemy w niniejszym artykule.

Względność czasu – opis zjawiska

Wyobraźmy sobie następującą sytuację: dwaj obserwatorzy poruszający się względem siebie ze stałą prędkością rejestrują za pomocą przyrządów pomiarowych odstęp czasu pomiędzy dwoma zdarzeniami. Czy wynik otrzymany przez każdego z obserwatorów będzie identyczny? Sprawdźmy to!

Załóżmy, że jeden z obserwatorów – Jacek, znajduje się w autobusie poruszającym się ze stałą prędkością względem drugiego obserwatora – Placka, który stoi na przystanku autobusowym. W pewnej chwili, Jacek używając ręcznego źródła światła wysyła pojedynczy impuls, który porusza się wzdłuż linii prostej prostopadle do kierunku ruchu autobusu, odbija się od zwierciadła umieszczonego w odległości L  od źródła światła i jest rejestrowany w tym samym punkcie, w którym nastąpiła jego emisja. Zdaniem Jacka odstęp czasu pomiędzy tymi dwoma zdarzeniami, a więc emisją i powrotem impulsu światła do źródła, wynosi Δt₀  i jest on związany z L  następującym wyrażeniem:

$$\Delta \hspace{.03cm} t_0 = \frac{2 \hspace{.05cm} L}{c}$$

gdzie c  to oczywiście prędkość światła w próżni równa 299 792 458 m/s.

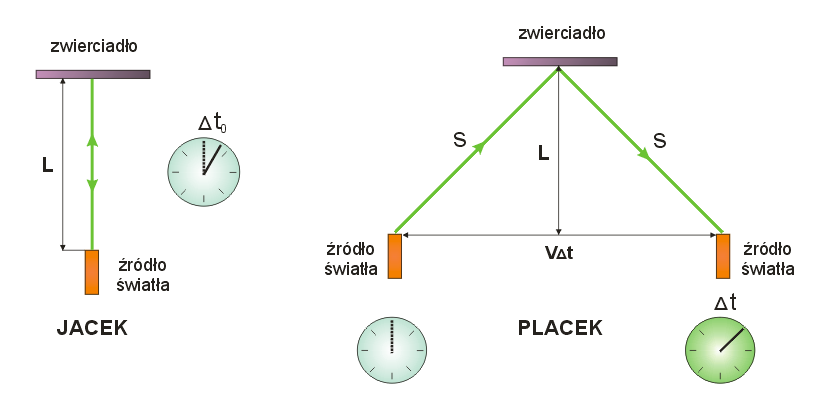
Zwróć uwagę (rysunek), że w układzie odniesienia związanym z Jackiem opisane zdarzenia zachodzą w tym samym miejscu i dlatego też pomiar odstępu czasu pomiędzy nimi wymaga użycia tylko jednego zegara.

A jak w takim razie zachodzące zdarzenia zinterpretuje Placek stojący na przystanku autobusowym, obok którego przejeżdża autobus? W układzie odniesienia związanym z Plackiem obydwa zdarzenia zachodzą w dwóch różnych miejscach w przestrzeni, wskutek czego pomiar odstępu czasu pomiędzy nimi będzie wymagał użycia dwóch zsynchronizowanych zegarów, po jednym dla każdego zdarzenia. Konsekwencją tego jest inny przebieg promieni świetlnych wychodzących i wracających do źródła (w porównaniu z układem odniesienia Jacka), w związku z czym różna jest także droga przebywana przez światło (zobacz rysunek). Czas Δt  zmierzony przez Placka będzie więc związany z drogą S, przebytą przez światło, poniższą zależnością:

$$\Delta \hspace{.03cm} t = \frac{2 \hspace{.05cm} S}{c}$$

Który pomiar jest poprawny?

Widzimy więc, że odstęp czasu zmierzony przez Jacka różni się od tego, który uzyskał Placek. Nasuwa się więc pytanie: który wynik jest poprawny? Jeżeli pomyślałeś, że wynik Jacka jest poprawny, to masz rację, jeżeli wskazałeś, że Placek to … też masz rację! Pomimo uzyskania dwóch zupełnie różnych odstępów czasu, zarówno Jacek i Placek mają rację! Dlaczego? Odpowiedź znajdziesz poniżej.

Spróbujmy powiązać ze sobą wyniki uzyskane przez Jacka i Placka. Zauważ, że zgodnie z powyższym rysunkiem drogę S  przebywaną przez promień świetlny możemy (korzystając z twierdzenia Pitagorasa) zapisać jako:

$$S = \sqrt{\mathstrut L^2 + \left( \tfrac{1}{2} \hspace{.05cm} V \hspace{.05cm} \Delta \hspace{.03cm} t \right)^2}$$

Jeżeli teraz w miejsce S  oraz L  podstawimy wyrażenia:

$$S = \tfrac{1}{2} \hspace{.05cm} c \hspace{.05cm} \Delta \hspace{.03cm} t \hspace{3cm} L = \tfrac{1}{2} \hspace{.05cm} c \hspace{.05cm} \Delta \hspace{.03cm} t_0$$

powstałe w wyniku przekształcenia wzorów definiujących odstęp czasu zmierzony przez Jacka i Placka oraz rozwiążemy otrzymane równanie względem Δt, otrzymamy poniższą zależność:

Względność czasu – wzór

$$\Delta \hspace{.03cm} t = \frac{\Delta \hspace{.03cm} t_0}{\sqrt{\mathstrut 1 \hspace{.1cm} – \hspace{.1cm} \left( \frac{V}{c} \right)^2}}$$

Za pomocą uzyskanego wyrażenia możemy porównywać czasy zmierzone przez poruszających się względem siebie obserwatorów. Zgodnie z postulatem stałej prędkości światła (zobacz: Postulaty szczególnej teorii względności Einsteina) wartość wektora prędkości musi być mniejsza od prędkości światła c, w związku z czym mianownik ułamka w powyższym wzorze będzie zawsze mniejszy od jedności. Dlatego też odstęp czasu Δt  zmierzony przez Placka jest dłuższy od czasu Δt₀, który uzyskał Jacek. Widzimy więc, że zależność pomiędzy czasem a przestrzenią jest różna dla obserwatorów poruszających się względem siebie oraz, że względny ruch (a więc prędkość z jaką się poruszamy) wpływa na szybkość upływu czasu pomiędzy zachodzącymi zdarzeniami (dlatego też odstęp czasu zmierzony przez Jacka – poruszającego się szybciej, niż Placek – jest krótszy w porównaniu z czasem zmierzonym przez Placka).

Warto wspomnieć, że odstęp czasu Δt₀, który jak pamiętamy jest czasem upływającym pomiędzy dwoma zdarzeniami zachodzącymi w tym samym punkcie układu odniesienia związanym z Jackiem, jest nazywany czasem własnym. Z kolei różnicę pomiędzy czasem Δt  a Δt₀  nazywamy dylatacją czasu. Słowo dylatacja oznacza wydłużenie, rozciągnięcie, dlatego też zjawisko to często funkcjonuje pod nazwą: wydłużenie (rozciągnięcie) czasu.