Prawo odbicia i załamania światła – zadanie nr 3

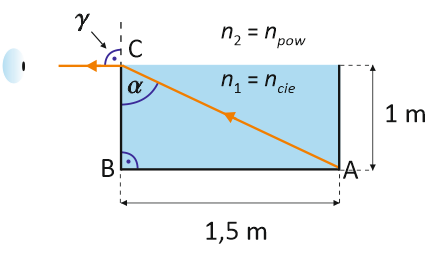
Do prostokątnego zbiornika wlano nieznaną ciecz, aż po sam jego wierzch. Kiedy obserwator patrzy z poziomu górnej powierzchni cieczy, widzi dolną krawędź A (zobacz rysunek). Oblicz współczynnik załamania światła w cieczy wiedząc, że kąt padania promienia świetlnego jest równy α , a kąt załamania γ  = 90^o. Załóż, że współczynnik załamania światła w powietrzu wynosi n_pow  = 1.

Aby wyznaczyć współczynnik załamania światła w cieczy skorzystamy z prawa załamania światła, nazywanego również prawem Snelliusa albo Snella. Zgodnie z tym prawem promień załamany leży w płaszczyźnie padania, a kąt załamania γ  związany jest z kątem padania α  poniższą zależnością:

$$n_1 \hspace{.1cm} \textrm{sin} \hspace{.05cm} \alpha = n_2 \hspace{.1cm} \textrm{sin} \hspace{.05cm} \gamma$$

gdzie:
n₁  – współczynnik załamania światła w pierwszym ośrodku (z którego pada światło),
n₂  – współczynnik załamania światła w drugim ośrodku (w którym rozchodzi się światło po przejściu przez powierzchnię rozgraniczającą dwa ośrodki),
α  – kąt padania światła,
γ  – kąt załamania światła.

W naszym przypadku n₁  odpowiada szukanemu współczynnikowi załamania światła w cieczy n_cie , z kolei n₂  – współczynnikowi załamania światła w powietrzu n_pow , zatem:

$$n_{cie} \hspace{.1cm} \textrm{sin} \hspace{.05cm} \alpha = n_{pow} \hspace{.1cm} \textrm{sin} \hspace{.05cm} \gamma$$

Korzystając z faktu,  że  $n_{pow} = 1$,  a  $\textrm{sin} \hspace{.05cm} \gamma = \textrm{sin} \hspace{.05cm} 90^\textrm{o}$ = 1, dostaniemy:

$$n_{cie} \hspace{.1cm} \textrm{sin} \hspace{.05cm} \alpha = 1 \hspace{1cm} \longrightarrow \hspace{1cm} n_{cie} = \frac{1}{\textrm{sin} \hspace{.05cm} \alpha}$$

Kąt padania α  nie jest znany. Aby go wyznaczyć skorzystamy z definicji funkcji sinus:

Zgodnie z powyższym rysunkiem:

$$\textrm{sin} \hspace{.05cm} \alpha = \frac{1,\hspace{-.1cm}5 \hspace{.05cm} \textrm{m}}{x}$$

gdzie x  to długość przeciwprostokątnej trójkąta ABC, która, zgodnie z twierdzeniem Pitagorasa, wynosi:

$$x^2 = \left( 1 \hspace{.05cm} \textrm{m} \right)^2 + \left( 1,\hspace{-.1cm}5 \hspace{.05cm} \textrm{m} \right)^2 \hspace{1cm} \longrightarrow \hspace{1cm} x = \sqrt{\left( 1 \hspace{.05cm} \textrm{m} \right)^2 + \left( 1,\hspace{-.1cm}5 \hspace{.05cm} \textrm{m} \right)^2} = 1,\hspace{-.1cm}8 \hspace{.05cm} \textrm{m}$$

Znając długość x, możemy przystąpić do obliczenia współczynnika załamania n_cie .

Podstawiając do równania $n_{cie} = \dfrac{1}{{\textrm{sin}} \hspace{.05cm} \alpha}$ wielkość  ${\textrm{sin}} \hspace{.05cm} \alpha = \dfrac{1,\hspace{-.1cm}5 \hspace{.1cm} {\textrm{m}}}{1,\hspace{-.1cm}8 \hspace{.1cm} {\textrm{m}}}$ otrzymamy wartość n_cie  równą:

$$n_{cie} = \frac{1}{\frac{1,5 \hspace{.05cm} \textrm{m}}{1,8 \hspace{.05cm} \textrm{m}}} = \frac{1,\hspace{-.1cm}8 \hspace{.1cm} \textrm{m}}{1,\hspace{-.1cm}5 \hspace{.1cm} \textrm{m}} = 1,\hspace{-.1cm}2$$