Prawo odbicia i załamania światła – zadanie nr 2

Wiązka światła rozchodząca się w powietrzu pada na płytkę szklaną pod kątem 30^o. Kąt, jaki tworzy z normalną padania wiązka rozchodząca się w szkle, wynosi 20^o. Oblicz współczynnik załamania światła w szkle. Załóż, że współczynnik załamania światła w powietrzu jest równy n_pow  = 1.

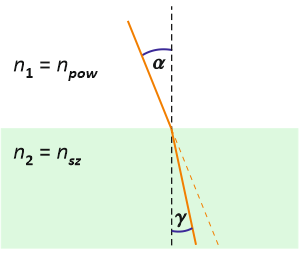
Zgodnie z treścią zadania promień świetlny rozchodząc się w powietrzu, pada na szklaną płytkę pod kątem α  = 30^o. Ze względu na różną wartość współczynnika załamania światła w powietrzu oraz w szkle, promień ten padając na granicę tych dwóch ośrodków ulega zjawisku załamania. Następstwem tego procesu jest zmiana kierunku ruchu promienia świetlnego w płytce szklanej, wyznaczona przez kąt załamania γ  = 20^o.

Aby obliczyć współczynnik załamania światła w szkle skorzystamy z prawa załamania światła, nazywanego również prawem Snelliusa albo Snella. Zgodnie z tym prawem promień załamany leży w płaszczyźnie padania, a kąt załamania γ  związany jest z kątem padania α  następującą zależnością:

$$n_1 \hspace{.05cm} \textrm{sin} \hspace{.05cm} \alpha = n_2 \hspace{.05cm} \textrm{sin} \hspace{.05cm} \gamma$$

gdzie:
n₁  – współczynnik załamania światła w ośrodku pierwszym (z którego pada światło),
n₂  – współczynnik załamania światła w ośrodku drugim (w którym rozchodzi się światło po przejściu przez powierzchnię rozgraniczającą dwa ośrodki),
α  – kąt padania światła,
γ  – kąt załamania światła.

W naszym przypadku n₁  odpowiada współczynnikowi załamania światła w powietrzu n_pow , z kolei n₂  – szukanemu współczynnikowi załamania światła w szkle n_sz . Mamy więc:

$$n_{pow} \hspace{.05cm} \textrm{sin} \hspace{.05cm} \alpha = n_{sz} \hspace{.05cm} \textrm{sin} \hspace{.05cm} \gamma$$

Ponieważ zarówno kąt α , jak i γ  są znane, dlatego po przekształceniu powyższego wzoru względem n_sz  otrzymamy:

$$n_{sz} = \frac{n_{pow} \hspace{.05cm} \textrm{sin} \hspace{.05cm} \alpha}{\textrm{sin} \hspace{.05cm} \gamma}$$

skąd po podstawieniu wartości liczbowych podanych w treści zadania dostaniemy:

$$n_{sz} = \frac{1 \cdot \hspace{.02cm} \textrm{sin} \hspace{.05cm} 30^\textrm{o}}{\textrm{sin} \hspace{.05cm} 20^\textrm{o}} = \frac{0,\hspace{-.1cm}5}{0,\hspace{-.1cm}34} = 1,\hspace{-.1cm}47$$