Załamanie światła. Prawo załamania światła

W tym artykule zajmiemy się uzupełnieniem opisu sytuacji przedstawionej w artykule Odbicie światła. Prawo odbicia światła o zjawisko załamania światła. Ponadto omówimy warunek zachodzenia tego zjawiska oraz podamy i poddamy analizie prawo załamania światła.

Załamanie światła – opis zjawiska

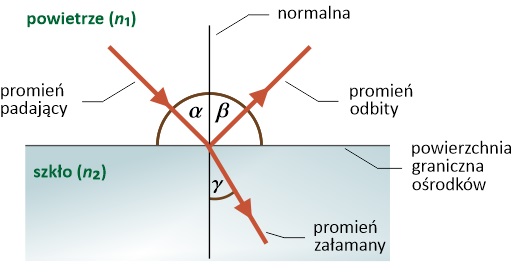
Gdy wiązka światła rozchodząca się w powietrzu pada na powierzchnię szklanej płytki, wówczas pewna część tej wiązki ulega odbiciu od powierzchni płytki, tworząc wiązkę odbitą skierowaną w prawo ku górze. Pozostała część padającej wiązki przechodzi przez płytkę i zaczyna się w niej rozchodzić, tworząc wiązkę załamaną, skierowaną w prawo ku dołowi. W związku z tym możemy napisać, że:

Jednym ze skutków zjawiska załamania jest zmiana kierunku rozchodzenia się światła (mówimy, że światło ulega odchyleniu). Jak się za chwilę przekonasz wyjątek od tej reguły stanowi sytuacja, w której światło pada prostopadle na powierzchnię szklanej płytki (lub innego ośrodka przezroczystego) oraz sytuacja, w której dwa ośrodki charakteryzują się jednakową wartością pewnej wielkości fizycznej nazywanej współczynnikiem załamania światła. Musisz pamiętać, że odchylenie od początkowego kierunku rozchodzenia się wiązki światła zachodzi tylko na granicy dwóch różnych ośrodków. Po przekroczeniu przez światło powierzchni granicznej światło nie ulega kolejnym załamaniom tylko rozchodzi się prostoliniowo, czyli po linii prostej.

Prawo załamania światła (prawo Snella)

Zgodnie z poniższym rysunkiem promień załamany, reprezentujący załamaną wiązkę światła, opisany jest przez kąt załamania γ. Wartość tego kąta podobnie jak kąta padania α  i kąta odbicia β, mierzona jest względem normalnej do powierzchni. Dla przypomnienia, normalna to prosta prostopadła do powierzchni granicznej ośrodków w punkcie odbicia i załamania światła. Zależność między kątem padania α  i załamania γ  opisuje prawo załamania światła:

n₁  i n₂  to wielkości fizyczne nazywane współczynnikami załamania światła. Wielkości te charakteryzują ośrodki, na granicy których zachodzi zjawisko załamania światła. Pierwsze poprawne rozumowanie dotyczące zjawiska załamania światła przeprowadził holenderski fizyk i astronom Willebrord Snel van Royen (1580 – 1626), dlatego też prawo załamania światła często nazywane jest prawem Snella albo Snelliusa.

Prawo załamania światła – analiza przypadków

Przekształcenie wzoru  $n_1 \hspace{.1cm} \textrm{sin} \hspace{.05cm} \alpha = n_2 \hspace{.1cm} \textrm{sin} \hspace{.05cm} \gamma$  do poniższej postaci

$$\textrm{sin} \hspace{.05cm} \gamma = \dfrac{n_1}{n_2} \hspace{.1cm} \textrm{sin} \hspace{.05cm} \alpha$$

pozwoli nam porównać kąt załamania γ  z kątem padania α. Zauważ, że wartość tych dwóch kątów zależy od stosunku współczynników załamania n₁ / n₂. W związku z powyższym możemy wyróżnić tu trzy sytuacje:

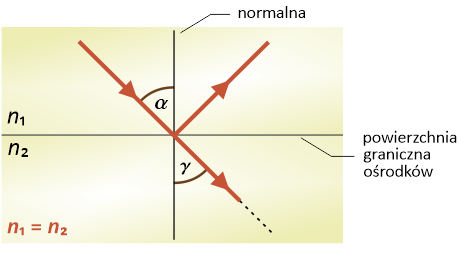
1. Gdy n₁  jest równe n₂  (n₁  = n₂ ), to sin γ  = sin α , a więc γ  = α  – kąt załamania jest równy kątowi padania światła. W takim przypadku zjawisko załamania nie zachodzi, w związku z czym promień padający po przejściu przez powierzchnię graniczną ośrodków nie będzie ulegał odchyleniu (załamaniu). Podobna sytuacja będzie mieć miejsce wtedy, gdy promień padający będzie padał prostopadle na granicę ośrodków (kąt padania i załamania będzie równy zero).



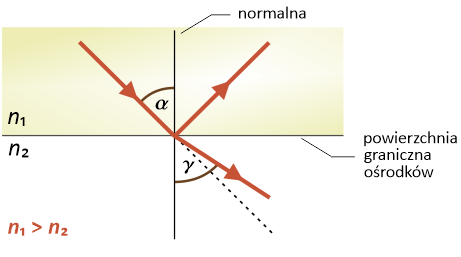
2. Gdy n₁  jest większe od n₂  (n₁  > n₂ ), to sin γ  > sin α , a więc kąt załamania γ  jest większy od kąta padania α  (γ  > α ). W takim przypadku promień świetlny przechodząc przez powierzchnię graniczną ośrodków będzie załamywany w stronę od normalnej tj. w stronę powierzchni granicznej ośrodków.



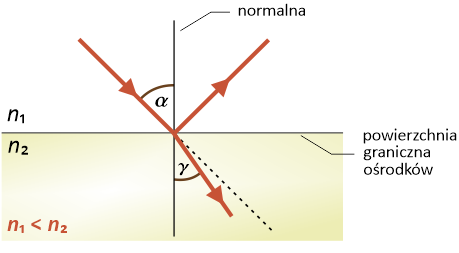
3. Gdy n₁  jest mniejsze od n₂  (n₁  < n₂ ), to sin γ  < sin α , a więc kąt załamania γ  jest mniejszy od kąta padania α  (γ  < α ). W takim przypadku promień świetlny przechodząc przez powierzchnię graniczną ośrodków będzie załamywany w stronę do normalnej.

Inny zapis prawa załamania światła

Ponieważ, jak napisalismy wyżej, podczas przechodzenia światła przez powierzchnię graniczną ośrodków zmianie ulega nie tylko kierunek rozchodzenia się światła, ale także jego prędkość oraz długość fali, dlatego też prawo załamania światła przedstawia się często w poniższej postaci:

$$\dfrac{\textrm{sin} \hspace{.05cm} \alpha}{\textrm{sin} \hspace{.05cm} \gamma} = \dfrac{V_{\hspace{.05cm}1}}{V_{\hspace{.08cm}2}} = \dfrac{\lambda_1}{\lambda_{\hspace{.05cm}2}}$$

gdzie:
V₁  i λ₁ to odpowiednio prędkość i długość fali światła w pierwszym ośrodku tj. ośrodku, z którego pada światło,
V₂  i λ₂ to odpowiednio prędkość i długość fali światła w drugim ośrodku tj. ośrodku, do którego przechodzi światło.

Więcej informacji na temat wpsółczynnika załamania znajdziesz w artykule Współczynnik załamania światła.

Aby dowiedzieć się więcej informacji na temat dziwacznych właściwości metamateriałów koniecznie przeczytaj artykuł Nowy rodzaj materiałów kurczących się pod wpływem … rozciągania.