Energia w ruchu harmonicznym – zadanie nr 5

Pionowa sprężyna rozciągnęła się o 15 cm po zawieszeniu na jej końcu ciężarka o masie 3 kg. Oblicz stałą sprężystości sprężyny. Następnie ciężarek przemieszczono o 5 cm w dół i puszczono go swobodnie. Wyznacz częstotliwość i amplitudę powstałych drgań oraz maksymalną prędkość ciężarka.

Sytuację opisaną w treści zadania przedstawia poniższy rysunek:

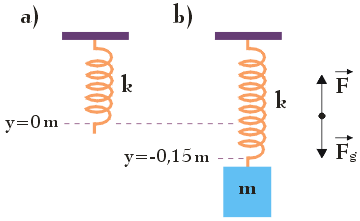
Przed zawieszeniem ciężarka na jednym z końców nierozciągniętej sprężyny, jej koniec znajduje się w punkcie y  = 0 m. Oś y  została tak dobrana, aby każde przemieszczenie końca sprężyny w kierunku dolnym odpowiadało ujemnej wartości na osi y. Wiemy, że po doczepieniu ciężarka o masie m  koniec sprężyny przemieszcza się w dół o 15 cm, zatem jego położenie na osi y  wynosi y  = – 0,15 m.

Aby wyznaczyć stałą sprężystości k  sprężyny skorzystamy z drugiej zasady dynamiki Newtona. Po doczepieniu ciężarka do sprężyny, układ sprężyna – ciężarek znajduje się w spoczynku, zatem skierowana w dół siła ciężkości $\vec{F}_g$  działająca na ciężarek (masę sprężyny zaniedbujemy) musi być równoważona przez skierowaną ku górze siłę sprężystości o wartości F  = – k y, przeciwstawiającą się dalszemu rozciągnięciu sprężyny. Sytuację tę możemy zapisać w poniższej formie:

$$F_g \hspace{.1cm} – \hspace{.1cm} F = 0 \hspace{1cm} \longrightarrow \hspace{1cm} mg \hspace{.15cm} – \hspace{.05cm} \left( \hspace{.1cm} – \hspace{.1cm} k \hspace{.05cm} y \right) = 0$$

skąd dostaniemy, że:

$$m \hspace{.05cm} g = \hspace{.1cm} – \hspace{.1cm} k \hspace{.05cm} y \hspace{1cm} \longrightarrow \hspace{1cm} k = \hspace{.1cm} – \hspace{.1cm} \frac{m \hspace{.05cm} g}{y}$$

Po podstawieniu do wzoru na k  wartości liczbowych oraz wykonaniu obliczeń, otrzymamy:

$$k = \hspace{.1cm} – \hspace{.1cm} \frac{3 \hspace{.05cm} \textrm{kg} \cdot 9,\hspace{-.1cm}81 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}^2}}{\hspace{.1cm} – \hspace{.1cm} 0,\hspace{-.1cm}15 \hspace{.05cm} \textrm{m}} = 196 \hspace{.05cm} \tfrac{\textrm{N}}{\textrm{m}}$$

Przejdźmy teraz do drugiej części zadania. Tym razem ciężarek (a więc i koniec sprężyny) przemieszczono o 5 cm w dół względem nowego położenia równowagi równego y  = – 0,15 m (sytuacja po zawieszeniu ciężarka), wywołując, po puszczeniu ciężarka, powstanie drgań harmonicznych.

Ponieważ klocek został swobodnie puszczony, całkowita energia mechaniczna układu klocek – sprężyna w momencie jego puszczenia była równa energii potencjalnej sprężystości sprężyny, zatem:

$$E = E_p \hspace{1cm} \longrightarrow \hspace{1cm} \tfrac{1}{2} \hspace{.05cm} k \hspace{.05cm} A^2 = \tfrac{1}{2} \hspace{.05cm} k \hspace{.05cm} x^2$$

Po skróceniu powyższego wyrażenia otrzymamy szukaną wartość amplitudy, równą:

$$A = x = 5 \hspace{.05cm} \textrm{cm}$$

Zauważ, że amplituda A  drgań odpowiada przemieszczeniu ciężarka (i tym samym sprężyny). Jest tak dlatego, ponieważ energia kinetyczna ciężarka w momencie jego swobodnego puszczenia była równa 0 J.

Częstotliwość i maksymalną prędkość drgań układu obliczymy korzystając z poniższej zależności:

$$\omega = \sqrt{\frac{\mathstrut k}{m}}$$

Wiemy, że  $\omega = 2 \hspace{.05cm} \pi \hspace{.05cm} f$, w związku z czym:

$$2 \hspace{.05cm} \pi \hspace{.05cm} f = \sqrt{\frac{\mathstrut k}{m}} \hspace{1cm} \longrightarrow \hspace{1cm} f = \frac{1}{2 \hspace{.05cm} \pi} \hspace{.05cm} \sqrt{\frac{\mathstrut k}{m}} = \frac{1}{2 \cdot 3,\hspace{-.1cm}14} \cdot \sqrt{\frac{196 \hspace{.05cm} \tfrac{\textrm{N}}{\textrm{m}}}{3 \hspace{.05cm} \textrm{kg}}} = 1,\hspace{-.1cm}3 \hspace{.05cm} \textrm{Hz}$$

Prędkość maksymalna V_max  jest wobec tego równa:

$$V_{max} = \omega \hspace{.05cm} A = \sqrt{\frac{\mathstrut k}{m}} \hspace{.05cm} A = \sqrt{\frac{196 \hspace{.05cm} \tfrac{\textrm{N}}{\textrm{m}}}{3 \hspace{.05cm} \textrm{kg}}} \cdot 0,\hspace{-.1cm}05 \hspace{.05cm} \textrm{m} = 0,\hspace{-.1cm}4 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}}$$