Prędkość i przyspieszenie w ruchu harmonicznym

Znając zależność przemieszczenia x(t)  ciała poruszającego się ruchem harmonicznym, możemy z łatwością obliczyć jego prędkość V(t).

Prędkość w ruchu harmonicznym

Różniczkując wyrażenie na x(t) :

$$V (t) = \frac{dx(t)}{dt} = \frac{d}{dt} \left[ A \hspace{.05cm} \textrm{cos} \left( \omega \hspace{.05cm} t + \varphi \right) \right]$$

otrzymamy:

$$V (t) = \hspace{.1cm} – \hspace{.1cm} \omega \hspace{.05cm} A \hspace{.05cm} \textrm{sin} \left( \omega \hspace{.05cm} t + \varphi \right)$$

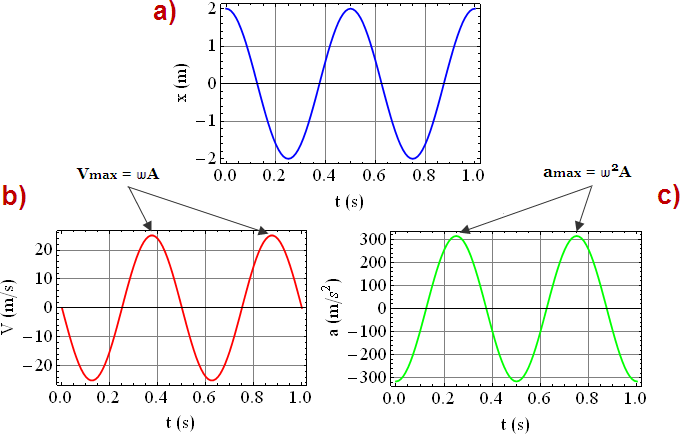
Wielkość ωA  stojąca przed funkcją sinusoidalną w powyższym wyrażeniu, będąca odpowiednikiem amplitudy A  we wzorze na przemieszczenie x(t), opisuje amplitudę zmian prędkości ciała, która dla przykładu przedstawionego na poniższym rysunku (rysunek b) wynosi ± ω A  = ± 25 m/s². Zwróć uwagę, że krzywa V(t)  jest przesunięta w lewo względem krzywej x(t)  o ćwierć okresu (π/2). Zauważ ponadto, że gdy przemieszczenie ciała osiąga maksymalną wartość równą amplitudzie A  drgań, prędkość ciała jest równa zero, z kolei, gdy przemieszczenie ciała wynosi zero, ciało osiąga maksymalną prędkość równą ± ω A.

Przyspieszenie w ruchu harmonicznym

Aby uzyskać wyrażenie opisujące przyspieszenie ciała w ruchu harmonicznym należy zróżniczkować wzór na V(t) :

$$a (t) = \frac{dV(t)}{dt} = \frac{d}{dt} \left[ \hspace{.1cm} – \hspace{.1cm} \omega \hspace{.05cm} A \hspace{.05cm} \textrm{sin} \left( \omega \hspace{.05cm} t + \varphi \right) \right]$$

otrzymując:

$$a(t) = \hspace{.1cm} – \hspace{.1cm} \omega^2 \hspace{.05cm} A \hspace{.05cm} \textrm{cos} \left( \omega \hspace{.05cm} t + \varphi \right)$$

Wielkość – ω²A  w powyższym wyrażeniu opisuje amplitudę zmian przyspieszenia ciała i jak widać na powyższym rysunku (rysunek c) przyspieszenie ciała zmienia się w zakresie ± ω²A  równym w przybliżeniu ± 320 m/s². Zauważ, że krzywa a(t)  jest przesunięta względem krzywych x(t)  i V(t)  odpowiednio o pół (π) oraz ćwierć okresu (π/2). W chwili, gdy przemieszczenie ciała osiąga wartość maksymalną +A, przyspieszenie ciała przyjmuje największą wartość ujemną – ω²A i odwrotnie. W przypadku, gdy przemieszczenie ciała jest równe zero, przyspieszenie również wynosi zero.

Podstawiając do zależności na a(t)  wyrażenie opisujące przemieszczenie ciała x(t)  w ruchu harmonicznym, dostaniemy:

$$a(t) = \hspace{.1cm} – \hspace{.1cm} \omega^2 x(t)$$

Z powyższego wzoru wynika bardzo ważna informacja: przyspieszenie ciała w ruchu harmonicznym jest proporcjonalne do jego przemieszczenia, przy czym ma ono przeciwny znak. Wielkość ω² spełnia rolę współczynnika proporcjonalności łączącego te dwie wielkości fizyczne.