Ruch harmoniczny – opis

Ruch harmoniczny to ruch okresowy, czyli ruch powtarzający się w regularnych odstępach czasu, w którym przemieszczenie x  ciała zmienia się w funkcji czasu t  w sposób sinusoidalny lub cosinusoidalny. Zależność przemieszczenia x (t )  ciała w ruchu harmonicznym opisuje poniższy wzór:

$$x (t) = A \hspace{.1cm} \textrm{cos} \left( \omega \hspace{.05cm} t + \varphi \right)$$

gdzie:
A  – amplituda drgań ciała,
ω  – częstość kołowa (kątowa) drgań,
φ  – początkowa faza drgań.

Wyrażenie $\left( \omega \hspace{.05cm} t + \varphi \right)$ nazywane jest fazą ruchu.

Amplituda drgań

Amplituda drgań A  to dodatnia stała, której wartość odzwierciedla wielkość siły, która wywołała drgania danego ciała. Im większa siła, tym większa amplituda drgań. W praktyce, amplituda drgań określa wartość maksymalnego wychylenia ciała z położenia równowagi. Funkcja cosinus, występująca w powyższym wyrażeniu, zmienia się w granicach ± 1, w związku z czym przemieszczenie ciała x (t )  może zmieniać się w przedziale ± A. Jednostką amplitudy jest jednostka długości w układzie SI, czyli metr (m).

Częstość kołowa i okres drgań

Częstość kołowa (kątowa) ω  opisuje szybkość, z jaką powtarza się zjawisko okresowe – w tym przypadku jedno pełne drganie ciała. Wielkość ta związana jest z okresem ruchu T, czyli czasem, w jakim wykonywane jest jedno pełne drganie ciała:

$$\omega = \frac{2 \hspace{.05cm} \pi}{T}$$

Jednostką częstości kołowej jest radian na sekundę (rad/s).

Częstotliwość drgań

Odwrotnością okresu T  jest częstotliwość f,  która opisuje liczbę pełnych drgań wykonywanych podczas każdej sekundy ruchu ciała:

$$f = \frac{1}{T}$$

Jednostką częstotliwości jest herc (Hz), związany z jednostką czasu – sekundą – poniższą zależnością:

$$1 \hspace{.05cm} \textrm{Hz} = \frac{1}{\textrm{s}}$$

Po podstawieniu zależności wiążącej okres T  z częstotliwością f  do wyrażenia na częstość kołową drgań ω, otrzymamy:

$$\omega = \frac{2 \hspace{.05cm} \pi}{T} = 2 \hspace{.05cm} \pi \hspace{.05cm} f$$

Początkowa faza drgań

Wartość stałej φ  nazywanej fazą początkową drgań zależy od położenia oraz prędkości ruchu ciała w chwili t  = 0. Niezerowa wartość stałej φ  (φ  ≠ 0) powoduje przesuwanie krzywej x (t )  (reprezentującej przemieszczenie ciała w funkcji czasu) w lewo (φ > 0) lub w prawo (φ  < 0).

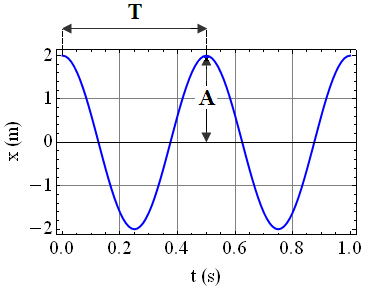
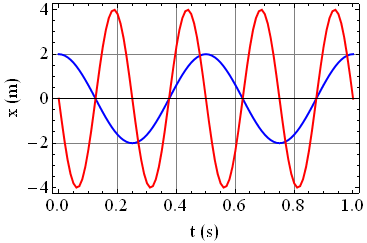
Ruch harmoniczny – przykładowe wykresy

Na poniższych rysunkach przedstawiono przykładową zależność przemieszczenia x  ciała w funkcji czasu t  oraz porównanie dwóch ruchów harmonicznych różniących się wartością amplitudy A, okresu T  oraz fazy początkowej drgań φ.