Siła w ruchu harmonicznym

Wprawienie dowolnego ciała w ruch wymaga przyłożenia siły o odpowiedniej wartości. Zgodnie z drugą zasadą dynamiki Newtona konsekwencją działania stałej siły na ciało o masie m  jest nadanie ciału stałego przyspieszenia a.  W przypadku ruchu harmonicznego wartość przyspieszenia a  nie jest stała, lecz, zgodnie z poniższym wzorem, ulega ciągłej zmianie w funkcji czasu:

$$a (t) = \hspace{.1cm} – \hspace{.1cm} \omega^2 \hspace{.05cm} x (t)$$

Zmienna wartość przyspieszenia oznacza, że siła F,  wywołująca ruch harmoniczny, jest siłą zmienną.

Siła w ruchu harmonicznym – wzór

Wartość siły w ruchu harmonicznym wyznaczymy w oparciu o drugą zasadę dynamiki Newtona:

$$\vec{F}_{wyp} = m \hspace{.05cm} \vec{a}$$

Wstawiając w miejsce a  zależność opisującą przyspieszenie ciała w ruchu harmonicznym, dostaniemy:

$$F (t) = \hspace{.1cm} – \hspace{.1cm} m \hspace{.05cm} \omega^2 \hspace{.05cm} x (t)$$

Zauważ, że siła działająca na ciało w ruchu harmonicznym jest proporcjonalna do jego przemieszczenia, lecz przeciwnie skierowana. Oznacza to, że podczas wychylenia ciała z położenia równowagi, siła ta zawsze zwrócona jest w stronę tego punktu. Poprzez analogię do wyrażenia opisującego prawo Hooke’a:

$$F = \hspace{.1cm} – \hspace{.1cm} k \hspace{.05cm} x$$

wielkość m ω², występująca we wzorze na F(t), odpowiada stałej k  nazywanej stałą sprężystości, której jednostką jest N/m:

$$k = m \hspace{.05cm} \omega^2$$

Częstość kołowa i okres drgań oscylatora harmonicznego

Zależność $k = m \hspace{.05cm} \omega^2$  jest bardzo pomocna w obliczaniu częstości kołowej drgań ω  układu drgającego składającego się np. z klocka o masie m  i sprężyny o stałej k  (masę sprężyny pomijamy), czy też struny gitary o masie m  i stałej k :

$$\omega = \sqrt{\frac{\mathstrut k}{m}}$$

W oparciu o powyższy wzór możemy także uzyskać wyrażenie na okres drgań T  takiego układu:

$$T = \frac{2 \hspace{.05cm} \pi}{\omega} = 2 \hspace{.05cm} \pi \hspace{.05cm} \sqrt{\frac{\mathstrut m}{k}}$$

Zwróć uwagę, że częstość ω  jest tym większa im większa jest wartość stałej sprężystości k  oraz im mniejsza jest masa m  ciała wykonującego drgania.

Każdy układ drgający, w którym siła jest liniowo proporcjonalna do przemieszczania ciała oraz przeciwnie do niego skierowana, nazywa się liniowym oscylatorem harmonicznym.

Zależność siły w funkcji czasu w ruchu harmonicznym – wykres

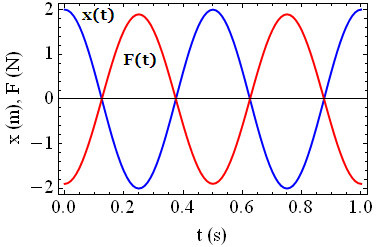
Na poniższym rysunku przedstawiono zależność przemieszczenia x(t)  (niebieska krzywa) oraz siły F(t)  (czerwona krzywa) dla ciała o masie m  = 6 g drgającego ruchem harmonicznym z amplitudą drgań A  = 2 m, okresem T  = 0,5 s i początkową fazą drgań φ  = 0. Zauważ, że zgodnie z tym co napisaliśmy wyżej, siła F  jest rzeczywiście proporcjonalna do wychylenia x  ciała z przeciwnym znakiem – siła wzrasta (maleje) wraz ze wzrostem (spadkiem) wychylenia, osiągając maksymalną wartość w punkcie maksymalnego wychylenia ciała oraz przyjmuje wartość zero, gdy położenie ciała odpowiada położeniu równowagi w zerze.