Zderzenie sprężyste ciał

Zderzenie sprężyste to zderzenie, w którym całkowita energia kinetyczna i całkowity pęd układu zderzających się ciał są zachowane. Pomimo, że zderzenia ciał spotykane na co dzień są zderzeniami niesprężystymi, to jednak niektóre z nich możemy w przybliżeniu traktować jako zderzenia sprężyste. Przykładem takiego zderzenia jest czołowe zderzenie dwóch kul bilardowych, podczas którego prawie cała energia kinetyczna jednej kuli zostaje przekazana początkowo nieruchomej drugiej kuli. W artykule tym zajmiemy się opisem zderzeń sprężystych odbywających się w układzie izolowanym tj. układzie, którego masa nie ulega zmianie w czasie, a wypadkowa sił zewnętrznych działających na układ ciał jest równa zero.

Zderzenie sprężyste dwóch poruszających się ciał tzw. zderzenie z ruchomą tarczą

Na rysunku a) i b) przedstawiono sytuację przed i po czołowym zderzeniu sprężystym dwóch ciał o różnych masach (m₁ > m₂) poruszających się w dodatnim kierunku osi x. Wskutek zderzenia prędkość ciała o masie m₁  zmienia się z $\vec{V}_1$  na  $\vec{V}’_{1}$  $\left( \vec{V}_1 > \vec{V}’_{1} \right)$, a prędkość ciała o masie m₂  z $\vec{V}_2$  na  $\vec{V}’_{2}$  $\left( \vec{V}_2 < \vec{V}’_{2} \right)$.

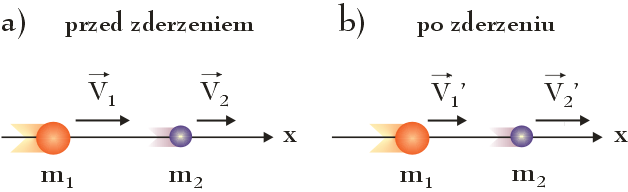
Zderzenie ciał zachodzi w układzie izolowanym (patrz wstęp artykułu), dlatego zgodnie z zasadą zachowania pędu całkowity początkowy pęd ciał  $\vec{p}_{cp}$  przed zderzeniem równy jest całkowitemu końcowemu pędowi ciał  $\vec{p}_{ck}$  po zderzeniu:

$$\vec{p}_{cp} = \vec{p}_{ck} \hspace{1cm} \longrightarrow \hspace{1cm} \vec{p}_{1p} + \vec{p}_{2p} = \vec{p}_{1k} + \vec{p}_{2k}$$

gdzie $\vec{p}_{1p}$  i  $\vec{p}_{2p}$  oraz  $\vec{p}_{1k}$  i  $\vec{p}_{2k}$  to odpowiednio początkowy i końcowy pęd ciała o masie m₁ i m₂.

Ponieważ ruch ciał przed i po zderzeniu odbywa się tylko w jednym kierunku tj. wzdłuż osi x, dlatego też w powyższym równaniu możemy opuścić strzałki nad wielkościami symbolizujące wektory:

$$p_{1p} + p_{2p} = p_{1k} + p_{2k}$$

Całkowita energia kinetyczna ciał $E_{kcp}$  przed zderzeniem równa jest całkowitej energii kinetycznej ciał $E_{kck}$  po zderzeniu, w związku z czym:

$$E_{kcp} = E_{kck} \hspace{1cm} \longrightarrow \hspace{1cm} E_{k1p} + E_{k2p} = E_{k1k} + E_{k2k}$$

gdzie $E_{k1p}$  i  $E_{k2p}$  oraz  $E_{k1k}$  i  $E_{k2k}$  to odpowiednio początkowa i końcowa energia kinetyczna ciała o masie m₁ i m₂.

Ponieważ  $p = m V$, a  $E_k = \frac{1}{2} m V^2$, dlatego zasada zachowania pędu i zasada zachowania energii dla tego układu ciał przyjmują ostatecznie następującą postać:

\begin{equation}
m_1 \hspace{.05cm} V_1 + m_2 \hspace{.05cm} V_2 = m_1 \hspace{.05cm} V’_1 + m_2 \hspace{.05cm} V’_2 \hspace{1cm} (1)
\end{equation}

oraz:

\begin{equation}
\tfrac{1}{2} \hspace{.05cm} m_1 \hspace{.05cm} V_1^2 + \tfrac{1}{2} \hspace{.05cm} m_2 \hspace{.05cm} V_2^2 = \tfrac{1}{2} \hspace{.05cm} m_1 \hspace{.05cm} V’^2_1 + \tfrac{1}{2} \hspace{.05cm} m_2 \hspace{.05cm} V’^2_2 \hspace{1cm} (2)
\end{equation}

Gdy znamy masy i prędkości początkowe obydwu ciał możemy w oparciu o równanie (1) i (2) wyznaczyć ich prędkości V’₁  i V’₂  po zderzeniu. Aby tego dokonać przekształcimy równanie (1) i (2) do poniższej postaci:

\begin{equation}
m_1 \left( V_1 \hspace{.15cm} – \hspace{.05cm} V’_1 \right) = m_2 \left( V’_2 \hspace{.15cm} – \hspace{.05cm} V_2 \right) \hspace{1cm} (3)
\end{equation}

oraz:

\begin{equation}
m_1 \left( V_1 \hspace{.15cm} – \hspace{.05cm} V’_1 \right) \left( V_1 + V’_1 \right) = m_2 \left( V’_2 \hspace{.15cm} – \hspace{.05cm} V_2 \right) \left( V’_2 + V_2 \right) \hspace{1cm} (4)
\end{equation}

(skorzystaliśmy z tożsamości $a^2 \hspace{.15cm} – \hspace{.05cm} b^2 = (a \hspace{.15cm} – \hspace{.05cm} b) (a + b)$ – dla przykładu:  $m_1 (V_1^2 \hspace{.15cm} – \hspace{.05cm} V’^2_1) = $ $m_1 (V_1 \hspace{.15cm} – \hspace{.05cm} V’_1) (V_1 + V’_1)$).

Dzieląc stronami równania (4) i (3), dostaniemy:

$$V_1 + V’_1 = V_2 + V’_2$$

Aby wyznaczyć prędkość V’₁  przekształćmy powyższe równanie względem prędkości V’₂ :

$$V’_2 = V_1 + V’_1 \hspace{.15cm} – \hspace{.05cm} V_2$$

Prędkość ciał po zderzeniu – wzory

Po podstawieniu wyrażenia na V’₂  do równania (3) oraz wykonaniu odpowiednich przekształceń, dostaniemy:

\begin{equation}
V’_1 = \frac{m_1 \hspace{.15cm} – \hspace{.05cm} m_2}{m_1 + m_2} \hspace{.05cm} V_1 + \frac{2 \hspace{.05cm} m_2}{m_1 + m_2} \hspace{.05cm} V_2 \hspace{1cm} (5)
\end{equation}

W analogiczny sposób możemy wyznaczyć wzór na prędkość V’₂ :

\begin{equation}
V’_2 = \frac{2 \hspace{.05cm} m_1}{m_1 + m_2} \hspace{.05cm} V_1 + \frac{m_2 \hspace{.15cm} – \hspace{.05cm} m_1}{m_1 + m_2} \hspace{.05cm} V_2 \hspace{1cm} (6)
\end{equation}

Zderzenie sprężyste ciała z nieruchomą tarczą

Skupmy się teraz na przypadku, w którym ciało o masie m₁  poruszające się z prędkością $\vec{V}_1$ zderza się czołowo i sprężyście ze spoczywającym ciałem o masie m₂, które możemy traktować jak nieruchomą tarczę (rysunek c i d).

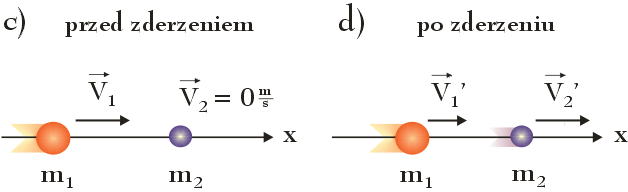
Zasada zachowania pędu dla tego układu ciał przybiera następującą postać:

$$m_1 \hspace{.05cm} V_1 = m_1 \hspace{.05cm} V’_1 + m_2 \hspace{.05cm} V’_2$$

a zasadę zachowania energii możemy zapisać jako:

$$\tfrac{1}{2} \hspace{.05cm} m_1 \hspace{.05cm} V_1^2 = \tfrac{1}{2} \hspace{.05cm} m_1 \hspace{.05cm} V’^2_1 + \tfrac{1}{2} \hspace{.05cm} m_2 \hspace{.05cm} V’^2_2$$

Prędkość ciał po zderzeniu – wzory

Dokonując podobnych przekształceń i podstawień, które przedstawiliśmy analizując zderzenie sprężyste dwóch poruszających się ciał, otrzymamy wzory na prędkość ciał po zderzeniu równe:

\begin{equation}
V’_1 = \frac{m_1 \hspace{.15cm} – \hspace{.05cm} m_2}{m_1 + m_2} \hspace{.05cm} V_1 \hspace{1cm} (7)
\end{equation}

oraz

\begin{equation}
V’_2 = \frac{2 \hspace{.05cm} m_1}{m_1 + m_2} \hspace{.05cm} V_1 \hspace{1cm} (8)
\end{equation}

Zwróć uwagę, że gdy m₁ > m₂  wyrażenie  $\dfrac{m_1 \hspace{.15cm} – \hspace{.05cm} m_2}{m_1 + m_2}$  we wzorze (7) jest zawsze dodatnie, a więc ciało o masie m₁  po zderzeniu będzie poruszać się bez zmiany swojego początkowego kierunku ruchu. Gdy m₁ < m₂  wyrażenie  $\dfrac{m_1 \hspace{.15cm} – \hspace{.05cm} m_2}{m_1 + m_2} < 0$, a więc ciało po zderzeniu będzie poruszać się w kierunku przeciwnym do początkowego (odbije się od nieruchomej tarczy). Wyrażenie  $\dfrac{2 \hspace{.05cm} m_1}{m_1 + m_2}$  występujące we wzorze (8) jest zawsze większe od zera, dlatego ciało o masie m₂  po zderzeniu będzie zawsze poruszać się w kierunku zgodnym z początkowym kierunkiem ruchu uderzającego w nie ciała.

Szczególne przypadki zderzeń sprężystych

1) Zderzenie ciał o jednakowych masach

Gdy zderzające się czołowo i sprężyście ciała mają jednakowe masy tj. m₁ = m₂ = m, równania (7) i (8) sprowadzają się do następującej postaci:

$$V’_1 = \frac{m \hspace{.15cm} – \hspace{.05cm} m}{2 \hspace{.05cm} m} \hspace{.05cm} V_1 = 0$$

$$V’_2 = \frac{2 \hspace{.05cm} m}{2 \hspace{.05cm} m} \hspace{.05cm} V_1 = V_1$$

Powyższe wzory odpowiadają sytuacji idealnego zderzenia dwóch kul bilardowych: uderzana bila zatrzymuje się, a początkowo nieruchoma bila (tarcza) uzyskuje prędkość równą początkowej prędkości uderzanej bili (bile „wymieniają się prędkościami”).

W ogólności, gdy dwa ciała o jednakowych masach, poruszające się z prędkością V₁  i V₂, ulegają czołowemu zderzeniu sprężystemu, mamy (zobacz wzór (5) i (6)):

$$V’_1 = V_2$$

$$V’_2 = V_1$$

2) Zderzenie z tarczą o bardzo dużej masie

Gdy tarcza posiada bardzo dużą masę tj.  m₁ ≪ m₂  równania (7) i (8) przyjmują poniższą postać:

$$V’_1 \approx \hspace{.15cm} – \hspace{.05cm} \frac{m_2}{m_2} \hspace{.05cm} V_1 \approx \hspace{.15cm} – \hspace{.05cm} V_1$$

$$V’_2 \approx 2 \hspace{.05cm} \frac{m_1}{m_2} \hspace{.05cm} V_1$$

Zgodnie z powyższymi wzorami ciało o masie m₁  zderzając się z ciałem o bardzo dużej masie, po prostu odbije się od niego (znak '-' stojący przed V₁  oznacza zmianę kierunku ruchu), bez zmiany początkowej wartości prędkości V₁. Z kolei ciało o masie m₂  będzie poruszać się w kierunku zgodnym z początkowym kierunkiem ruchu ciała o masie m₁, lecz jego prędkość będzie bardzo mała, ponieważ $\dfrac{2 m_1}{m_2} \ll 1$.

3) Zderzenie z tarczą o bardzo małej masie

Gdy ciało wystrzelone w kierunku tarczy posiada bardzo dużą masę tj.  m₁ ≫ m₂  równania (7) i (8) przedstawiają się następująco:

$$V’_1 \approx \frac{m_1}{m_1} \hspace{.05cm} V_1 \approx V_1$$

$$V’_2 \approx 2 \hspace{.05cm} \frac{m_1}{m_1} \hspace{.05cm} V_1 \approx 2 \hspace{.05cm} V_1$$

Z powyższych równań wynika, że wskutek zderzenia ciało o masie m₁  będzie poruszać się z praktycznie niezmienioną wartością prędkości, z zachowaniem swojego początkowego kierunku ruchu, a ciało o masie m₂  będzie poruszać się z prędkością dwukrotnie większą od prędkości ciała o masie m₁.