Zderzenie niesprężyste ciał

Straty energii występujące podczas zderzenia niesprężystego powodują, że tylko całkowity pęd układu zderzających się ciał jest zachowany (całkowita energia kinetyczna układu nie jest zachowana, ponieważ przyjmuje ona różną wartość przed i po zderzeniu). Aby omówić zderzenie niesprężyste ciał wyobraźmy sobie układ izolowany, w którym dwa ciała o masach m₁ i m₂, przy czym m₁ > m₂, poruszają się w dodatnim kierunku osi x (rysunek a).

Zderzenie niesprężyste dwóch poruszających się ciał tzw. zderzenie z ruchomą tarczą

Ciało o masie m₁  porusza się z prędkością V₁, a ciało o masie m₂  z prędkością V₂, przy czym V₁ > V₂. Po upływie pewnego czasu ciała te ulegają czołowemu zderzeniu niesprężystemu, którego następstwem jest zmiana wartości prędkości obydwu ciał: ciała o masie m₁  z V₁  na V’₁, a ciała o masie m₂  z V₂  na V’₂ (rysunek b).

Zmianie wartości prędkości ciał towarzyszy zmiana ich energii kinetycznej oraz pędu. Ponieważ energia kinetyczna w zderzeniach niesprężystych nie jest zachowana, dlatego aby wyznaczyć prędkość ciał po zderzeniu skorzystamy z zasady zachowania pędu. Zgodnie z tą zasadą całkowity początkowy pęd ciał  $\vec{p}_{cp}$  przed zderzeniem musi być równy całkowitemu końcowemu pędowi ciał  $\vec{p}_{ck}$  po zderzeniu:

$$\vec{p}_{cp} = \vec{p}_{ck} \hspace{1cm} \longrightarrow \hspace{1cm} \vec{p}_{1p} + \vec{p}_{2p} = \vec{p}_{1k} + \vec{p}_{2k}$$

gdzie $\vec{p}_{1p}$  i  $\vec{p}_{2p}$  oraz  $\vec{p}_{1k}$  i  $\vec{p}_{2k}$  to odpowiednio początkowy i końcowy pęd ciała o masie m₁ i m₂.

Ponieważ ruch ciał przed i po zderzeniu odbywa się tylko w jednym kierunku (wzdłuż osi x), dlatego też w powyższym równaniu możemy opuścić strzałki symbolizujące wektory i zapisać je w następującej postaci:

$$p_{1p} + p_{2p} = p_{1k} + p_{2k}$$

Pęd ciała wynosi  $p = m V$, dlatego:

$$m_1 \hspace{.05cm} V_1 + m_2 \hspace{.05cm} V_2 = m_1 \hspace{.05cm} V’_1 + m_2 \hspace{.05cm} V’_2$$

Prędkość ciał po zderzeniu – wzory

Jeżeli oprócz mas i prędkości początkowych obydwu ciał, znamy przynajmniej jedną z ich prędkości końcowych (V’₁  lub V’₂) możemy na podstawie powyższego wzoru obliczyć prędkość końcową drugiego ciała. Gdy znamy prędkość V’₂, mamy:

$$V’_1 = \frac{m_2 \left( V_2 \hspace{.15cm} – \hspace{.05cm} V’_2 \right) + m_1 \hspace{.05cm} V_1}{m_1}$$

a gdy znamy prędkość V’₁ :

$$V’_2 = \frac{m_1 \left( V_1 \hspace{.15cm} – \hspace{.05cm} V’_1 \right) + m_2 \hspace{.05cm} V_2}{m_2}$$

Zderzenie niesprężyste ciała z nieruchomą tarczą

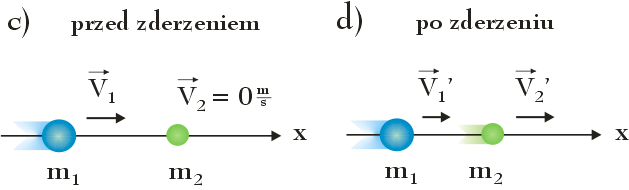
Omówmy teraz przypadek, w którym ciało o masie m₁  poruszające się z prędkością V₁  zderza się czołowo i niesprężyście ze spoczywającym ciałem o masie m₂, które możemy traktować jak nieruchomą tarczę (rysunek c i d).

Zasada zachowania pędu dla tego układu ciał przybiera następującą postać:

$$m_1 \hspace{.05cm} V_1 = m_1 \hspace{.05cm} V’_1 + m_2 \hspace{.05cm} V’_2$$

Prędkość ciał po zderzeniu – wzory

Jeżeli oprócz mas i prędkości początkowych obydwu ciał, znamy przynajmniej jedną z ich prędkości końcowych (V’₁  lub V’₂), możemy na podstawie powyższego wzoru obliczyć prędkość końcową drugiego ciała. Gdy znamy prędkość V’₂, mamy:

$$V’_1 = \frac{m_1 \hspace{.05cm} V_1 \hspace{.15cm} – \hspace{.05cm} m_2 \hspace{.05cm} V’_2}{m_1}$$

a gdy znamy prędkość V’₁ :

$$V’_2 = \frac{m_1 \left( V_1 \hspace{.15cm} – \hspace{.05cm} V’_1 \right)}{m_2}$$

Zderzenie doskonale niesprężyste

Cechą charakterystyczną zderzenia doskonale niesprężystego jest przyleganie do siebie ciał po zderzeniu. Wskutek tego zderzenia ciało (lub układ kilku ciał) traci większą część lub całość posiadanej energii kinetycznej. W ramach opisu zderzenia doskonale niesprężystego rozważymy dwa przypadki: pierwszy z nich będzie dotyczył sytuacji, w której obydwa ciała poruszają się z pewnymi prędkościami w tym samym kierunku, drugi – gdy jedno z ciał spoczywa, a drugie porusza się w jego kierunku.

Pierwszy przypadek

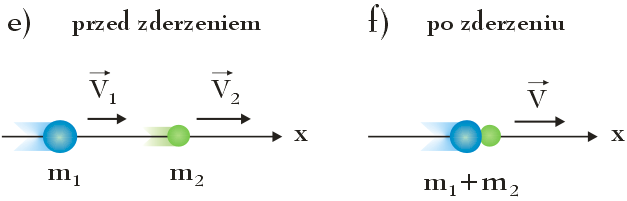
Na rysunku e) i f) przedstawiono sytuację przed i po doskonale niesprężystym czołowym zderzeniu dwóch ciał poruszających się w tym samym kierunku wzdłuż osi x. Przed zderzeniem prędkość ciała o masie m₁  jest równa V₁, a prędkość ciała o masie m₂  wynosi V₂, przy czym V₁ > V₂. Po zderzeniu układ ciał o masie m = m₁ + m₂  porusza się z prędkością V.

Z zasady zachowania pędu zapisanej dla tego układu, mamy:

$$m_1 \hspace{.05cm} V_1 + m_2 \hspace{.05cm} V_2 = \left( m_1 + m_2 \right) V$$

Prędkość V  wynosi w związku z powyższym:

$$V = \frac{m_1}{m_1 + m_2} \hspace{.05cm} V_1 + \frac{m_2}{m_1 + m_2} \hspace{.05cm} V_2$$

Drugi przypadek

Sytuacja podobna do pierwszego przypadku, z tym, że ciało o masie m₂  spoczywa (V₂ = 0 m/s). Korzystając z powyższego wzoru na prędkość V  układu ciał, otrzymamy:

$$V = \frac{m_1}{m_1 + m_2} \hspace{.05cm} V_1$$