Ruch obrotowy – opis

Mechanika klasyczna - teoria
Brak komentarzy
Drukuj

Ruch opon samochodowych, kół zębatych czy wskazówek zegara na tarczy zegarowej to przykłady ruchu obrotowego. Ruch obrotowy dowolnego ciała zachodzi wokół pewnej osi nazywanej osią obrotu. Gdy położenie osi obrotu nie ulega zmianie w czasie (jak w przypadku ruchu wskazówek zegara) mówimy wówczas o ruchu obrotowym wokół stałej osi obrotu. W przeciwnym razie tj. gdy oś obrotu zmienia swoje położenie, mówimy o ruchu wokół zmiennej osi obrotu (jak w przypadku opon samochodowych). W artykule tym omówimy podstawowe wielkości fizyczne opisujące ruch obrotowy bryły sztywnej tj. ciała, którego kształt nie ulega zmianie podczas obrotów.

Położenie kątowe

Aby określić położenie ciała w ruchu obrotowym korzystamy z wielkości fizycznej nazywanej położeniem kątowym. Położenie kątowe α  to kąt, jaki tworzy linia odniesienia tj. linia prostopadła do osi obrotu, obracająca się wraz z ciałem, z pewnym stałym wybranym przez nas kierunkiem, któremu domyślnie przypisujemy zerowe położenie kątowe.

ruch obrotowy ciała wokół stałej pionowej osi obrotu - rysunek schematyczny - ruch obrotowy - opis
Ruch obrotowy bryły sztywnej wokół pionowej, stałej osi obrotu (oś z układu współrzędnych), odbywający się w kierunku ruchu wskazówek zegara. Każdy punkt bryły porusza się po okręgu, którego środek leży na osi obrotu. Niebieska linia odpowiada linii odniesienia.

Położenie kątowe α  możemy mierzyć np. względem dodatniego kierunku osi x (zobacz: poniższy rysunek). Korzystając z definicji miary łukowej kąta, mamy:

$$\alpha = \frac{l}{r}$$

gdzie:
l  – długość łuku okręgu (zielona linia) zawartego między zerowym położeniem kątowym ciała (osią x) a linią odniesienia,
r  – promień okręgu (czerwona linia).

położenie i przemieszczenie kątowe ciała - rysunek schematyczny - ruch obrotowy - opis
Przekrój ciała płaszczyzną prostopadłą do osi obrotu (czarna kropka). Położenie kątowe obracającego się ciała wyznacza kąt zawarty między zerowym położeniem kątowym (oś x) a linią odniesienia (niebieska, ciągła linia).

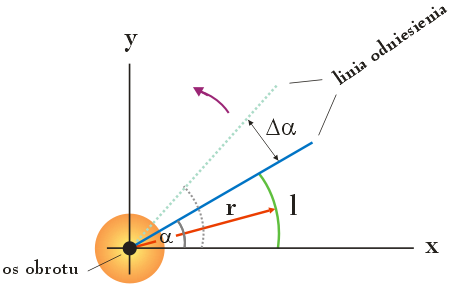
Długość łuku l  jest proporcjonalna do długości promienia r, dlatego miara łukowa kąta nie zależy od długości promienia. Jednostką położenia kątowego α  jest radian, oznaczany w skrócie jako rad. Obwód okręgu wynosi $2 \hspace{.05cm} \pi \hspace{.05cm} r$, w związku z czym kąt pełny (360o) wynosi $2 \hspace{.05cm} \pi$ radianów. Oznacza to, że:

$$1 \hspace{.05cm} \textrm{rad} = 57,\hspace{-.1cm}3^{\textrm{o}}$$

Ważna uwaga
Położenie kątowe α  po każdym pełnym obrocie ciała nie ulega „wyzerowaniu”. Po jednym pełnym obrocie $\alpha = 2 \pi \hspace{.05cm} \textrm{rad}$, po dwóch pełnych obrotach $\alpha = 4 \hspace{.05cm} \pi \hspace{.05cm} \textrm{rad}$ itd.

Przemieszczenie kątowe

Jeżeli podczas obrotu położenie kątowe ciała zmienia się z α1 na α2, to przemieszczenie kątowe Δα  ciała wynosi:

$$\Delta \hspace{.03cm} \alpha = \alpha_2 \hspace{.15cm} – \hspace{.05cm} \alpha_1$$

gdzie:
α1 – położenie kątowe ciała w chwili t1 (niebieska, ciągła linia na powyższym rysunku),
α2 – położenie kątowe ciała w chwili t2 (jasnoniebieska, przerywana linia na powyższym rysunku).

Przemieszczenie kątowe Δα  może przyjmować wartość dodatnią lub ujemną, w zależności od kierunku obrotu ciała:

Przemieszczenie kątowe ciała – dobór znaku
Jeżeli ciało obraca się w kierunku zgodnym z kierunkiem ruchu wskazówek zegara, przemieszczenie kątowe Δα  jest ujemne, a jeżeli obrót zachodzi w kierunku przeciwnym do kierunku ruchu wskazówek zegara, przemieszczenie kątowe Δα  jest dodatnie.
Ważna uwaga
W zakresie bardzo małych przemieszczeń, przemieszczeniu kątowemu Δα  możemy przypisać wektor. Jednak w ogólnym przypadku, przemieszczenie kątowe Δα , pomimo posiadania wartości, kierunku oraz zwrotu, nie jest wielkością wektorową, ponieważ nie spełnia wszystkich praw działań na wektorach. Okazuje się bowiem, że suma kilku wektorów przemieszczenia kątowego zależy od kolejności ich dodawania, co sprawia, że wielkość ta nie może być wektorem.

Prędkość kątowa (częstość kołowa)

Jeżeli chcemy opisać prędkość ciała obracającego się wokół pewnej ustalonej osi obrotu korzystamy z wielkości nazywanej prędkością kątową lub częstością kołową, oznaczaną małą grecką literą omega – ω.

Gdy znamy przemieszczenie kątowe Δα  ciała zachodzące w przedziale czasu Δt możemy obliczyć średnią prędkość kątową ωsr ciała, zdefiniowaną jako:

$$\omega_{sr} = \frac{\alpha_2 \hspace{.15cm} – \hspace{.05cm} \alpha_1}{t_2 \hspace{.15cm} – \hspace{.05cm} t_1} = \frac{\Delta \hspace{.03cm} \alpha}{\Delta \hspace{.03cm} t}$$

gdzie α1 i α2 to odpowiednio położenie kątowe ciała w chwili t1 i t2.

Jeżeli interesuje nas z kolei prędkość ciała w pewnej ustalonej chwili czasu mówimy wówczas o chwilowej prędkości kątowej albo po prostu o prędkości kątowej ω, którą obliczamy z poniższego wzoru:

$$\omega = \lim\limits_{\Delta t \rightarrow 0} \hspace{.02cm} \frac{\Delta \hspace{.03cm} \alpha}{\Delta \hspace{.03cm} t} = \frac{d\alpha}{dt}$$

gdzie wyrażenie  $\dfrac{d \alpha}{dt}$  to pochodna funkcji α(t ) względem czasu t.

Jednostką prędkości kątowej jest radian na sekundę (rad/s) lub obrót na sekundę (obr/s).

Prędkość kątowa ciała jest wielkością wektorową. Wektor prędkości kątowej $\vec{\omega}$ skierowany jest wzdłuż osi obrotu ciała, a jego zwrot wyznaczamy stosując regułę prawej dłoni:

Reguła prawej dłoni – wyznaczanie zwrotu wektora prędkości kątowej
Jeżeli palce prawej dłoni będą wskazywać kierunek obrotu ciała, to odchylony kciuk wskaże nam zwrot wektora prędkości kątowej $\vec{\omega}$.
prędkość kątowa obracającego się ciała - wartość dodatnia i ujemna - rysunek schematyczny - ruch obrotowy - opis
Ruch obrotowy ciała wokół stałej, pionowej osi obrotu z: a) gdy ciało obraca się w kierunku zgodnym z kierunkiem ruchu wskazówek zegara, prędkość kątowa ω  jest ujemna (ω  < 0), b) gdy ruch ciała zachodzi w kierunku przeciwnym do ruchu wskazówek zegara, prędkość kątowa ω  jest dodatnia (ω  > 0).

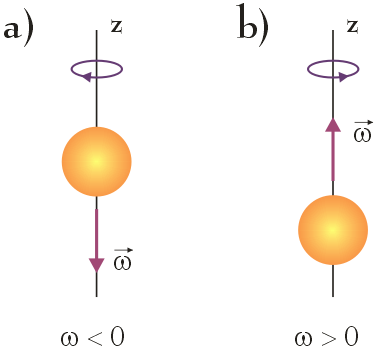
Ruch obrotowy ciała zachodzi nie w kierunku, a wokół kierunku wektora $\vec{\omega}$, który wyznacza oś obrotu ciała. Jeżeli ciało porusza się w kierunku zgodnym z kierunkiem ruchu wskazówek zegara przyjmujemy, że prędkość kątowa ω  jest ujemna, a jeżeli w kierunku przeciwnym do ruchu wskazówek zegara, przyjmujemy, że prędkość kątowa ω  jest dodatnia.

Ważna uwaga
Gdy ruch obrotowy ciała odbywa się wokół stałej osi obrotu, możemy pominąć zapis wektorowy i zapisywać prędkość kątową ciała jako ω. Ruch ciała wokół stałej osi obrotu może zachodzić tylko w dwóch kierunkach (zgodnie i przeciwnie do ruchu wskazówek zegara), do rozróżnienia których wystarczy nam znak plus albo minus.

Przyspieszenie kątowe

Gdy prędkość kątowa ciała ulega zmianie w czasie, to ciało posiada pewne przyspieszenie kątowe oznaczane małą grecką literą epsilon – ε. Średnie przyspieszenie kątowe obracającego się ciała wynosi:

$$\varepsilon_{sr} = \frac{\omega_2 \hspace{.15cm} – \hspace{.05cm} \omega_1}{t_2 \hspace{.15cm} – \hspace{.05cm} t_1} = \frac{\Delta \hspace{.03cm} \omega}{\Delta \hspace{.03cm} t}$$

gdzie ω1 i ω2 to odpowiednio prędkość kątowa ciała w chwili t1 i t2.

Chwilowe przyspieszenie kątowe albo po prostu przyspieszenie kątowe ε  jest z kolei zdefiniowane jako:

$$\varepsilon = \lim\limits_{\Delta t \rightarrow 0} \hspace{.02cm} \frac{\Delta \hspace{.03cm} \omega}{\Delta \hspace{.03cm} t} = \frac{d\omega}{dt}$$

gdzie wyrażenie  $\dfrac{d \omega}{dt}$  to pochodna funkcji ω(t ) względem czasu t.

Przyspieszenie kątowe, podobnie jak prędkość kątowa, jest wielkością wektorową. Jednostką przyspieszenia kątowego jest radian na sekundę kwadrat (rad/s2) albo obrót na sekundę kwadrat (obr/s2).

Ważna uwaga
Powyższe wzory na prędkość kątową i przyspieszenie kątowe obracającego się ciała można stosować zarówno do ciała sztywnego traktowanego jako całość, jak i do każdej jego cząstki.

Tagi:

Dodaj komentarz