Moment bezwładności

Moment bezwładności, oznaczany literą I, to wielkość fizyczna charakterystyczna dla ruchu obrotowego ciała. Wielkość ta przyjmuje stałą wartość dla danego ciała i określonej osi jego obrotu. Wartość momentu bezwładności zależy od masy ciała, położenia osi obrotu, wokół której obraca się ciało oraz od rozkładu (rozmieszczenia) jego masy. Można więc napisać, że moment bezwładności ciała informuje nas o tym, jak rozłożona jest masa obracającego się ciała wokół ustalonej osi jego obrotu. Im większa wartość momentu bezwładności, tym trudniej jest wprawić albo zmienić ruch obrotowy danego ciała (np. zmniejszyć lub zwiększyć jego prędkość kątową).

Oś obrotu, a moment bezwładności ciała

Poniższy rysunek ilustruje jak wybór osi obrotu ciała wpływa na wartość jego momentu bezwładności i tym samym na łatwość/trudność wprawienia go w ruch obrotowy. Na rysunku a) i b) przedstawiono jednorodny walec o promieniu r  i wysokości h  wykonujący obroty wokół osi podłużnej (rysunek a)) oraz wokół osi prostopadłej do walca, przechodzącej przez jego środek (rysunek b)).

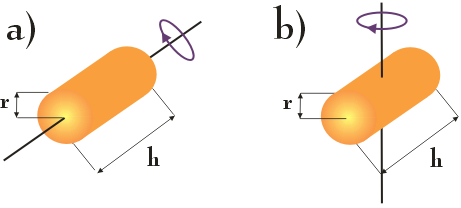
W obydwu przypadkach mamy do czynienia z tym samym ciałem, lecz to właśnie w pierwszym przypadku (rysunek a)) łatwiej jest wprawić walec w ruch obrotowy. Przyczyną tej sytuacji jest różny rozkład masy walca wokół osi jego obrotu: podczas obrotu walca wokół osi podłużnej masa walca jest bardziej skupiona w pobliżu osi obrotu, niż w przypadku drugim. Skutkiem tego jest mniejsza wartość momentu bezwładności walca z rysunku a), aniżeli walca z rysunku b).

Moment bezwładności pojedynczej cząstki

Aby obliczyć moment bezwładności I  pojedynczej cząstki obracającej się wokół określonej osi obrotu korzystamy z następującego wyrażenia:

$$I = m \hspace{.05cm} r^2$$

gdzie:
m  – masa cząstki,
r  – odległość cząstki od osi obrotu.

Jednostką momentu bezwładności jest kg ⋅ m².

Moment bezwładności ciała złożonego z n cząstek

Moment bezwładności ciała składającego się z n  cząstek jest równy sumie momentów bezwładności każdej z cząstek względem określonej osi obrotu:

$$I = \sum\limits_{i=1}^n m_i \hspace{.05cm} r_i^2$$

Na przykład dla ciała składającego się z czterech cząstek, mamy:

$$I = \sum\limits_{i=1}^4 m_i \hspace{.05cm} r_i^2 = m_1 \hspace{.05cm} r_1^2 + m_2 \hspace{.05cm} r_2^2 + m_3 \hspace{.05cm} r_3^2 + m_4 \hspace{.05cm} r_4^2$$

gdzie:
m₁, m₂, m₃  i m₄ – masy cząstek, z których składa się ciało,
r₁, r₂, r₃  i r₄ – odległość od osi obrotu odpowiednio cząstki o masie m₁, m₂, m₃  i m₄.

Moment bezwładności ciała rozciągłego

Gdy ciało składa się z bardzo wielu cząstek położonych blisko siebie, sumę momentów bezwładności w powyższym równaniu zastępujemy całką. Jeżeli ciało rozciągłe podzielimy na nieskończenie małe elementy o masie dm  odległe od osi obrotu o wielkość r, to moment bezwładności I  będzie równy:

$$I = \int r^2 \hspace{.05cm} dm$$

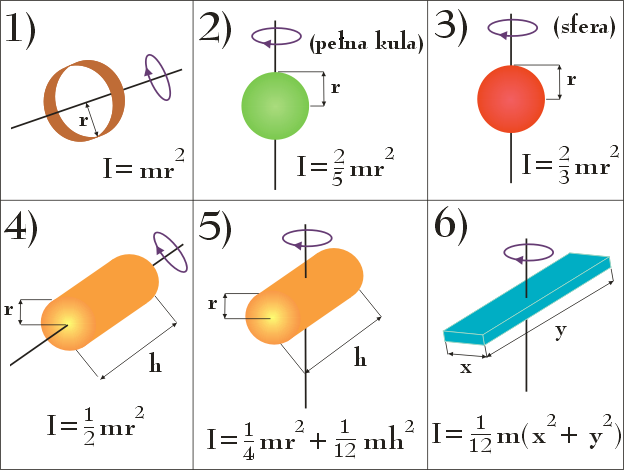
Na poniższym rysunku przedstawiono wybrane ciała rozciągłe wraz z podaniem ich momentów bezwładności, obliczonych dla zaznaczonych na rysunkach osiach obrotu: