Twierdzenie Steinera

Gdy chcemy obliczyć moment bezwładności ciała rozciągłego względem pewnej osi obrotu możemy skorzystać ze wzoru $I = \displaystyle\int r^2 \hspace{.05cm} \rm dm$. Jeżeli znamy jednak moment bezwładności tego ciała względem osi równoległej do danej osi i przechodzącej przez środek jego masy możemy to zrobić o wiele łatwiej korzystając z twierdzenia Steinera. Treść tego twierdzenia, sformułowanego przez szwajcarskiego matematyka Jakoba Steinera (1796 – 1863), brzmi następująco:

Twierdzenie Steinera – definicja

Matematyczny zapis twierdzenia Steinera wyraża się następująco:

$$I = I_0 + m \hspace{.05cm} d^2$$

gdzie:
I – szukany moment bezwładności ciała względem osi obrotu równoległej do danej osi i przechodzącej przez środek jego masy,
I₀  – moment bezwładności ciała względem osi obrotu przechodzącej przez środek jego masy,
m – masa ciała,
d – odległość między osiami obrotu.

Z powyższego równania wynika bardzo cenna informacja: moment bezwładności danego ciała przyjmuje najmniejszą wartość wtedy, gdy oś jego obrotu przechodzi przez środek jego masy (zauważ, że gdy d = 0, moment bezwładności ciała wynosi $I = I_0$).

Twierdzenie Steinera – przykład

Moment bezwładności I₀  walca o masie m, promieniu r  i wysokości h  = 4 r  względem osi obrotu prostopadłej do walca, przechodzącej przez środek jego masy (czarna linia na poniższym rysunku) wynosi $I_0 = \tfrac{1}{4} m \hspace{.05cm} r^2 + \tfrac{1}{12} m \hspace{.05cm} h^2$. Ile wynosi moment bezwładności I  walca względem osi równoległej do podanej osi (czerwona linia na poniższym rysunku), oddalonej od niej o wielkość d  = r, gdzie r  to promień walca?

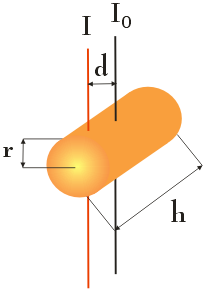
Oś obrotu walca, dla której mamy obliczyć moment bezwładności I,  jest równoległa do osi przechodzącej przez środek jego masy, w związku z czym do obliczenia I  wykorzystamy twierdzenie Steinera. Wiemy, że $I_0 = \tfrac{1}{4} m \hspace{.05cm} r^2 + \tfrac{1}{12} m \hspace{.05cm} h^2$. Wiemy także, że h = 4 r, dlatego:

$$I_0 = \tfrac{1}{4} m \hspace{.05cm} r^2 + \tfrac{1}{12} m \hspace{.05cm} \cdot \hspace{.05cm} \left( 4 \hspace{.05cm} r \right)^2 = \tfrac{1}{4} m \hspace{.05cm} r^2 + \tfrac{4}{3} m \hspace{.05cm} r^2 = \tfrac{19}{12} \hspace{.05cm} m \hspace{.05cm} r^2$$

Masa walca jest równa m a odległość między osiami obrotu wynosi d = r. Po podstawieniu wartości I₀  oraz d do wzoru opisującego twierdzenie Steinera, otrzymamy:

$$I = I_0 + m \hspace{.05cm} d^2 = \tfrac{19}{12} \hspace{.05cm} m \hspace{.05cm} r^2 + m \hspace{.05cm} r^2 = \tfrac{31}{12} \hspace{.05cm} m \hspace{.05cm} r^2$$