Siła w ruchu harmonicznym – zadanie nr 3

Klocek o ciężarze 30 N umocowano do górnego końca równi pochyłej, nachylonej pod kątem φ  = 45^o, za pomocą sprężyny o stałej sprężystości k  = 100 N/m. Wiedząc, że długość nierozciągniętej sprężyny wynosi L  = 0,4 m oblicz, w jakiej odległości l  od górnego końca równi klocek pozostaje w spoczynku. Siły tarcia pomijamy.

Przed umocowaniem klocka do sprężyny, jej długość L  wynosi 0,4 m – długość ta odpowiada zarazem odległości dzielącej górny koniec równi od dolnego końca nierozciągniętej sprężyny. Po doczepieniu klocka o ciężarze 30 N, długość sprężyny ulega oczywiście wydłużeniu. Im większy ciężar klocka, tym większe rozciągnięcie sprężyny. Aby obliczyć wartość tego wydłużenia (i tym samym odległość klocka od górnego końca równi) skorzystamy z drugiej zasady dynamiki Newtona.

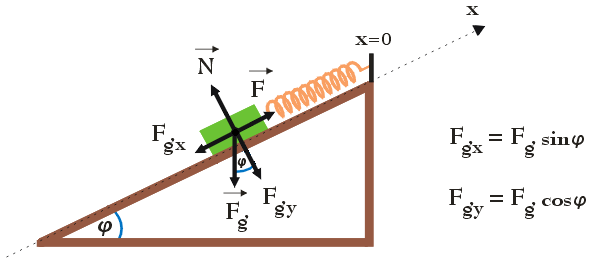
Zgodnie z powyższym rysunkiem ruch klocka wzdłuż osi x  (równoległej do powierzchni równi pochyłej) odbywa się za pośrednictwem dwóch sił. Jedną z tych sił jest składowa F_gx  siły ciężkości równa F_g  sin φ, drugą natomiast – siła sprężystości F  sprężyny równa -k x. Wiemy, że klocek po zamocowaniu go do dolnego końca sprężyny pozostaje w stanie spoczynku, w związku z czym siły F_gx  oraz F  działające na klocek muszą się równoważyć. Innymi słowy wypadkowa siła działająca na klocek jest równa zero:

$$F_{gx} \hspace{.1cm} – \hspace{.1cm} \left( \hspace{.1cm} – \hspace{.1cm} k \hspace{.05cm} x \right) = 0 \hspace{1cm} \longrightarrow \hspace{1cm} m \hspace{.05cm} g \hspace{.05cm} \textrm{sin} \hspace{.05cm} \varphi = \hspace{.1cm} – \hspace{.1cm} k \hspace{.05cm} x$$

Przekształcając powyższe wyrażenie względem przemieszczenia x  klocka, otrzymamy:

$$x = \hspace{.1cm} – \hspace{.1cm} \frac{m \hspace{.05cm} g \hspace{.05cm} \textrm{sin} \hspace{.05cm} \varphi}{k} = \hspace{.1cm} – \hspace{.1cm} \frac{30 \hspace{.05cm} \textrm{N} \cdot \textrm{sin} \hspace{.05cm} 45^\textrm{o}}{100 \hspace{.05cm} \frac{\textrm{N}}{\textrm{m}}} = \hspace{.1cm} – \hspace{.1cm} 0,\hspace{-.1cm}21 \hspace{.05cm} \textrm{m}$$

Ujemna wartość przemieszczenia x  jest zgodna z przyjętą konwencją, w której oś x  dobraliśmy w taki sposób, aby przemieszczeniu klocka w dół równi odpowiadała wartość ujemna (zobacz rysunek).

Znając wartość przemieszczenia klocka (i tym samym rozciągnięcia sprężyny), wynoszącego ponad połowę początkowej długości L  nierozciągniętej sprężyny, możemy obliczyć odległość l  klocka od górnego końca równi pochyłej:

$$l = L + x = \hspace{.1cm} – \hspace{.1cm} 0,\hspace{-.1cm}4 \hspace{.05cm} \textrm{m} + \left( \hspace{.1cm} – \hspace{.1cm} 0,\hspace{-.1cm}21 \hspace{.05cm} \textrm{m} \right) = \hspace{.1cm} – \hspace{.1cm} 0,\hspace{-.1cm}61 \hspace{.05cm} \textrm{m}$$