Druga zasada dynamiki Newtona – zadanie nr 2

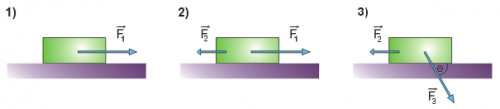
Na ciało o masie m = 3 kg mogące poruszać się bez tarcia po poziomej powierzchni (wzdłuż umownej osi x) działa jedna lub dwie siły (zobacz rysunek). Dwie pierwsze siły o wartościach F₁  = 6 N i F₂  = 3 N skierowane są wzdłuż osi x, z kolei trzecia siła o wartości F₃  = 2 N działa na ciało pod kątem Θ  = 60^o. Oblicz przyspieszenie doznawane przez to ciało dla każdego z trzech przypadków przedstawionych na poniższym rysunku.

Zależność pomiędzy przyspieszeniem doznawanym przez dowolne ciało wskutek działającej na nie siły wypadkowej opisuje druga zasada dynamiki Newtona:

$$\vec{F}_{wyp} = m \hspace{.1cm} \vec{a}$$

Siła oraz przyspieszenie są wielkościami wektorowymi posiadającymi trzy składowe przestrzenne: x, y  oraz z  (np. dla przyspieszenia mamy: a_x , a_y , a_z ). Jednak, jak wynika z treści zadania, ciało porusza się tylko wzdłuż jednej osi – osi x , dlatego też interesują nas tylko „iksowe” składowe siły (F_x ) oraz przyspieszenia (a_x ). W związku z tym faktem, powyższy wzór możemy zapisać w następującej postaci:

$$F_{wyp, x} = m \hspace{.1cm} a_{wyp, x}$$

Po przekształceniu powyższego wzoru względem przyspieszenia dostaniemy:

$$a_{wyp,x} = \frac{F_{wyp,x}}{m}$$

Przypadek 1)

W pierwszym przypadku, na ciało działa tylko jedna siła skierowana wzdłuż osi x , w związku z czym siła wypadkowa działająca na to ciało jest równa właśnie tej sile: $F_{wyp,x} = F_1$. Mamy więc:

$$a_{wyp,x} = \frac{F_{wyp,x}}{m} = \frac{F_1}{m} = \frac{6 \hspace{.1cm} \rm{N}}{3 \hspace{.1cm} \rm{kg}} = 2 \hspace{.1cm} \tfrac{\rm m}{\rm s^2}$$

Przypadek 2)

W drugim przypadku, na ciało działają dwie siły poziome $\vec{F_1}$ oraz $\vec{F_2}$, zwrócone w przeciwnych kierunkach. Siła wypadkowa działająca na to ciało jest równa różnicy tych sił:

$${F}_{wyp,x} = F_1 \hspace{.1cm} – \hspace{.1cm} F_2$$

W tym przypadku, przyspieszenie doznawane przez ciało będzie równe:

$$a_{wyp,x} = \frac{F_{wyp,x}}{m} = \frac{F_1 \hspace{.1cm} – \hspace{.1cm} F_2}{m} = \frac{6 \hspace{.1cm} \rm{N} \hspace{.1cm} – \hspace{.1cm} 3 \hspace{.1cm} \rm{N}}{3 \hspace{.1cm} \rm{kg}} = 1 \hspace{.1cm} \tfrac{\rm m}{\rm s^2}$$

Przypadek 3)

W trzecim przypadku, na ciało oprócz siły $\vec{F_2}$ działa także siła $\vec{F_3}$ skierowana pod kątem 60^o względem poziomu. Pamiętamy, że ciało porusza się wzdłuż osi x , w związku z czym interesuje nas tylko „iksowa” składowa tej siły (F_3,x ), zgodna z kierunkiem ruchu ciała. Składowa ta jest równa:

$$F_{3,x} = F_3 \hspace{.1cm} \rm{cos} \hspace{.05cm} \theta$$

Wypadkowa siła działająca na to ciało wynosi:

$${F}_{wyp,x} = F_{3,x} \hspace{.1cm} – \hspace{.1cm} F_2 = F_3 \hspace{.1cm} \textrm{cos} \hspace{.05cm} \theta \hspace{.1cm} – \hspace{.1cm} F_2$$

a przyspieszenie doznawane przez to ciało wskutek działania tej siły jest równe:

$$a_{wyp,x} = \frac{F_3 \hspace{.1cm} \textrm{cos} \hspace{.05cm} \theta \hspace{.1cm} – \hspace{.1cm} F_2}{m} = \frac{2 \hspace{.1cm} \rm{N} \hspace{.05cm} \cdot \hspace{.05cm} \rm{cos} \hspace{.05cm} 60^{\rm o} \hspace{.1cm} – \hspace{.1cm} 3 \hspace{.1cm} \rm{N}}{3 \hspace{.1cm} \rm{kg}} = \hspace{.1cm} – \hspace{.1cm} \tfrac{2}{3} \hspace{.1cm} \tfrac{\rm m}{\rm s^2}$$