Skrócenie długości – zadanie nr 4

Pręt o długości dwóch metrów tworzy z osią x’, związaną z układem odniesienia W’, kąt 60^o. Układ W’  porusza się równolegle względem układu W  z prędkością 0,95 c. Oblicz jaką długość pręta zmierzy nieruchomy obserwator w układzie W.

Zgodnie z treścią zadania układ W’  porusza się względem układu W  z prędkością V  = 0,95 c. Długość pręta, równa 2 metry, zmierzona w układzie odniesienia W’  jest długością spoczynkową L₀  pręta, ponieważ względem tego układu położenie pręta nie ulega zmianie (zobacz: Skrócenie długości). Szukaną wielkością jest więc długość L  pręta, jaką zmierzy obserwator związany z układem odniesienia W. Zależność pomiędzy L₀  a L  opisuje poniższa relacja:

$$L = L_0 \hspace{.1cm} \sqrt{1 \hspace{.15cm} – \hspace{.05cm} \left( \tfrac{V}{c} \right)^2}$$

Musimy jednak pamiętać, że efekt skrócenia długości występuje tylko i wyłącznie w przypadku obiektów poruszających się w kierunku równoległym do kierunku wektora względnej prędkości dwóch układów odniesienia (innymi słowy w kierunku równoległym do kierunku ruchu). W naszym przypadku pręt tworzy z osią x’  układu W’  kąt 60^o, w związku z czym według pomiarów dokonanych przez obserwatora w układzie W, tylko składowa x  pręta tj. równoległa do kierunku ruchu ulegnie skróceniu. Długość składowej y, prostopadłej do kierunku ruchu, nie ulegnie zmianie. Sytuacja ta została schematycznie przedstawiona na poniższym rysunku:

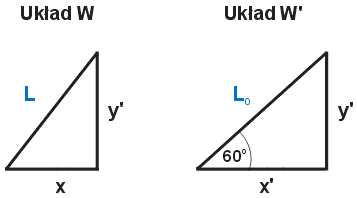
Obliczmy zatem długości składowych pręta zmierzonych w układzie odniesienia W’  korzystając z definicji funkcji trygonometrycznych sinusa oraz cosinusa:

$$\textrm{cos} \hspace{.05cm} 60^{\textrm{o}} = \frac{x’}{L_0} \hspace{1cm} \longrightarrow \hspace{1cm} x’ = L_0 \hspace{.05cm} \textrm{cos} \hspace{.1cm} 60^{\textrm{o}} = 2 \hspace{.05cm} \textrm{m} \cdot 0,\hspace{-.1cm}5 = 1 \hspace{.05cm} \textrm{m}$$

$$\textrm{sin} \hspace{.05cm} 60^{\textrm{o}} = \frac{y’}{L_0} \hspace{1cm} \longrightarrow \hspace{1cm} y’ = L_0 \hspace{.05cm} \textrm{sin} \hspace{.1cm} 60^{\textrm{o}} = 2 \hspace{.05cm} \textrm{m} \cdot \frac{\sqrt{\mathstrut 3}}{2} = \sqrt{\mathstrut 3} \hspace{.05cm} \textrm{m}$$

Długość składowej x, jaką zmierzy obserwator związany z układem W  będzie równa:

$$x = x’ \sqrt{1 \hspace{.15cm} – \hspace{.05cm} \left( \tfrac{V}{c} \right)^2} = 1 \hspace{.05cm} \textrm{m} \cdot \sqrt{1 \hspace{.15cm} – \hspace{.05cm} \left( \frac{0,95 \hspace{.05cm} c}{c} \right)^2} = 0,\hspace{-.1cm}31 \hspace{.05cm} \textrm{m}$$

Znając długość składowej x  pręta oraz wiedząc, że y  = y’  otrzymamy długość L  pręta, równą:

$$L = \sqrt{x^2 + y^2} = \sqrt{\left( 0,\hspace{-.1cm}31 \hspace{.05cm} \textrm{m} \right)^2 + \left( \sqrt{\mathstrut 3} \hspace{.05cm} \textrm{m} \right)^2} = 1,\hspace{-.1cm}76 \hspace{.05cm} \textrm{m}$$