Siła wyporu. Prawo Archimedesa – zadanie nr 5

Oblicz z jakim przyspieszeniem wypływa z wody kulka o gęstości ρ_k  = 800 kg/m³. Opory ruchu pomijamy. Gęstość wody wynosi 1000 kg/m³.

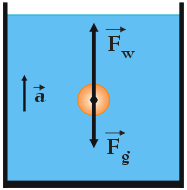
Kulka porusza się ku powierzchni wody, a więc wartość siły wyporu $\vec{F}_w$  (skierowanej również ku górze) działającej na kulkę ze strony płynu musi być większa od wartości siły ciężkości $\vec{F}_g$, skierowanej ku dołowi. Wypadkowa tych dwóch sił powoduje ruch kulki z pewnym przyspieszeniem $\vec{a}$, którego wartość musimy znaleźć. Zgodnie z drugą zasadą dynamiki Newtona mamy:

$$\vec{F}_{wyp} = m_k \hspace{.05cm} \vec{a} \hspace{1cm} \longrightarrow \hspace{1cm} \vec{F}_{wyp} = \vec{F}_w \hspace{.1cm} – \hspace{.1cm} \vec{F}_g = m_k \hspace{.05cm} \vec{a}$$

gdzie:
$\vec{F}_{wyp}$  – siła wypadkowa działająca na kulkę,
m_k  – masa kulki.

Korzystając z definicji siły wyporu i siły ciężkości, otrzymamy:

$$m_w \hspace{.05cm} g \hspace{.15cm} – \hspace{.05cm} m_k \hspace{.05cm} g = m_k \hspace{.05cm} \vec{a}$$

gdzie m_w  to masa wody wypartej przez kulkę.

Wartości obydwu mas nie są podane w treści zadania. Możemy je jednak z łatwością wyznaczyć korzystając z definicji gęstości płynów, zgodnie z którą masę dowolnego obiektu możemy przedstawić jako iloczyn jego gęstości oraz objętości:

$$V_w \hspace{.05cm} \rho_w \hspace{.05cm} g \hspace{.15cm} – \hspace{.05cm} V_k \hspace{.05cm} \rho_k \hspace{.05cm} g = V_k \hspace{.05cm} \rho_k \hspace{.05cm} a$$

Do momentu wypłynięcia kulki na powierzchnię wody objętość V_w  wody będzie równa objętości V_k  kulki, w związku z czym:

$$V_k \hspace{.05cm} \rho_w \hspace{.05cm} g \hspace{.15cm} – \hspace{.05cm} V_k \hspace{.05cm} \rho_k \hspace{.05cm} g = V_k \hspace{.05cm} \rho_k \hspace{.05cm} a \hspace{1cm} \longrightarrow \hspace{1cm} a = \frac{g \left( \rho_w \hspace{.15cm} – \hspace{.05cm} \rho_k \right)}{\rho_k} = g \left( \frac{\rho_w}{\rho_k} \hspace{.1cm} – \hspace{.1cm} 1 \right)$$

Po podstawieniu do powyższego wyrażenia wartości liczbowych oraz wykonaniu obliczeń, dostaniemy:

$$a = 9,\hspace{-.1cm}81 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}^2} \cdot \left( \frac{1000 \hspace{.05cm} \tfrac{\textrm{kg}}{\textrm{m}^3}}{800 \hspace{.05cm} \tfrac{\textrm{kg}}{\textrm{m}^3}} \hspace{.1cm} – \hspace{.1cm} 1 \right) = 2,\hspace{-.1cm}5 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}^2}$$