Siła wyporu. Prawo Archimedesa – zadanie nr 3

Jaki ułamek objętości góry lodowej pływającej po morzu stanowi część widoczna ponad powierzchnią wody? Gęstość wody morskiej oraz lodu jest znana i wynosi odpowiednio 1024 kg/m³ oraz 917 kg/m³.

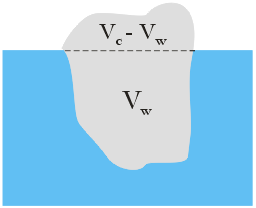
Załóżmy, że całkowita objętość góry lodowej wynosi V_c . Jeżeli następnie objętość góry lodowej znajdującą się pod powierzchnią wody oznaczymy poprzez V_pw , wówczas objętość góry widoczna nad wodą będzie równa V_c  – V_pw . W związku z tym szukany ułamek objętości v  będzie wynosić:

$$v = \frac{V_c \hspace{.15cm} – \hspace{.05cm} V_{pw}}{V_c}$$

Objętość niewidocznej części góry lodowej V_pw , znajdującej się pod powierzchnią wody, odpowiada objętości V_w  wody wypartej przez tą część góry, dlatego też powyższe równanie możemy zapisać jako:

$$v = \frac{V_c \hspace{.15cm} – \hspace{.05cm} V_w}{V_c} = 1 \hspace{.15cm} – \hspace{.05cm} \frac{V_w}{V_c}$$

Wartość objętości V_c  i V_w  nie jest znana. Korzystając z faktu, że góra lodowa pływa w wodzie, możemy je jednak z łatwością wyznaczyć. Gdy ciało pływa w płynie siła ciężkości równoważona jest przez siłę wyporu (zobacz: Siła wyporu. Prawo Archimedesa), zatem:

$$F_w = F_g \hspace{1cm} \longrightarrow \hspace{1cm} m_w \hspace{.05cm} g = m_c \hspace{.05cm} g$$

gdzie:
m_w  – masa wody morskiej wyparta przez górę lodową,
m_c  – masa góry lodowej.

Masy m_w  i m_c  nie są wprawdzie znane, jednak możemy je wyznaczyć korzystając z definicji gęstości:

$$V_w \hspace{.05cm} \rho_w \hspace{.05cm} g = V_c \hspace{.05cm} \rho_c \hspace{.05cm} g$$

Po skróceniu i przekształceniu, dostaniemy:

$$\frac{V_w}{V_c} = \frac{\rho_c}{\rho_w}$$

Podstawiając powyższą zależność do wzoru na ułamek objętości góry lodowej oraz wstawiając wartości gęstości podane w treści zadania i wykonując obliczenia, otrzymamy:

$$v = 1 \hspace{.1cm} – \hspace{.1cm} \frac{V_w}{V_c} = 1 \hspace{.1cm} – \hspace{.1cm} \frac{\rho_c}{\rho_w} = 1 \hspace{.1cm} – \hspace{.1cm} \frac{917 \hspace{.05cm} \tfrac{\textrm{kg}}{\textrm{m}^3}}{1024 \hspace{.05cm} \tfrac{\textrm{kg}}{\textrm{m}^3}} = 0,\hspace{-.1cm}1$$

Tak więc część góry lodowej znajdująca się nad powierzchnią wody stanowi 10% jej całkowitej objętości.