Siła w ruchu harmonicznym – zadanie nr 1

Pewien oscylator liniowy składa się z klocka o masie 2 kg umocowanego na sprężynie o stałej sprężystości k. Po wprawieniu układu klocek – sprężyna w drgania o amplitudzie A  = 0,15 m, jego ruch powtarza się co 0,2 s. Oblicz częstość kołową, stałą sprężystości, maksymalną prędkość oraz maksymalną siłę, z jaką sprężyna działa na klocek.

Sytuację opisaną w treści zadania przedstawia poniższy rysunek.

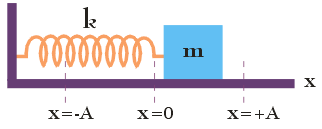
Pod wpływem zewnętrznej siły, układ klocek – sprężyna zaczyna drgać ruchem harmonicznym z amplitudą A  = 0,15 m i okresem T  = 0,2 s. Częstość kołowa drgań ω, której wartość należy wyznaczyć, związana jest z okresem T  poniższą zależnością:

$$\omega = \frac{2 \hspace{.05cm} \pi}{T}$$

Po podstawieniu do powyższego wzoru wartości liczbowych oraz wykonaniu obliczeń, dostaniemy:

$$\omega = \frac{2 \cdot 3,\hspace{-.1cm}14}{0,\hspace{-.1cm}2 \hspace{.1cm} \textrm{s}} = 31,\hspace{-.1cm}4 \hspace{.05cm} \tfrac{\textrm{rad}}{\textrm{s}}$$

W oparciu o wielkości ω  i m, których wartości są znane, możemy obliczyć stałą sprężystości k  sprężyny:

$$k = m \hspace{.05cm} \omega^2 = 2 \hspace{.05cm} \textrm{kg} \cdot \left( 31,\hspace{-.1cm}4 \hspace{.05cm} \tfrac{\textrm{rad}}{\textrm{s}} \right)^2 = 1972 \hspace{.05cm} \tfrac{\textrm{N}}{\textrm{m}}$$

Prędkość maksymalna ciała w ruchu harmonicznym wyraża się poprzez iloczyn amplitudy A  oraz częstości kołowej drgań ω. Obydwie te wielkości są znane, zatem:

$$V_{max} = \omega \hspace{.05cm} A = 31,\hspace{-.1cm}4 \hspace{.05cm} \tfrac{\textrm{rad}}{\textrm{s}} \cdot 0,\hspace{-.1cm}15 \hspace{.05cm} \textrm{m} = 4,\hspace{-.1cm}7 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}}$$

Wartość siły, z jaką sprężyna oddziałuje na klocek zależy od stopnia jej rozciągnięcia (innymi słowy od przemieszczenia klocka). Maksymalne przemieszczenie ciała w ruchu harmonicznym odpowiada amplitudzie A  drgań (x  = ± A), w związku z czym maksymalna wartość siły F, wynosi:

$$F = \hspace{.1cm} – \hspace{.1cm} k \cdot \left( \hspace{.1cm} – \hspace{.1cm} A \right) = k \hspace{.05cm} A = 1972 \hspace{.05cm} \tfrac{\textrm{N}}{\textrm{m}} \cdot 0,\hspace{-.1cm}15 \hspace{.05cm} \textrm{m} = 296 \hspace{.05cm} \textrm{N}$$