Prędkość i przyspieszenie w ruchu harmonicznym – zadanie nr 4

Oblicz średnią prędkość w ruchu harmonicznym, dla którego amplituda drgań A  = 0,02 m, okres T  = 1 s, a początkowa faza drgań φ  = 0.

Zgodnie z poniższą zależnością wartość prędkości ciała drgającego ruchem harmonicznym zależy od amplitudy A, częstości kołowej ω, początkowej fazy drgań φ  oraz od parametru t  reprezentującego czas:

$$V (t) = \hspace{.1cm} – \hspace{.1cm} \omega \hspace{.05cm} A \hspace{.05cm} \textrm{sin} \left( \omega \hspace{.05cm} t + \varphi \right)$$

Zależność V(t)  dla parametrów ruchu podanych w treści zadania przedstawia poniższy rysunek:

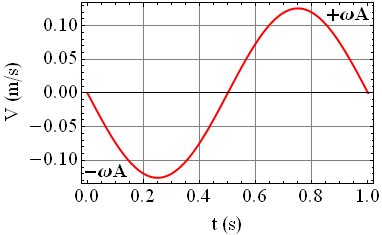
Zwróć uwagę, że podczas okresu T  drgań, wartość V  zmienia się w przedziale ± ωA, przyjmując zarówno wartości ujemne, jak i wartości dodatnie. Prędkość średnią V_sr , z jaką porusza się ciało podczas okresu T, obliczymy korzystając z poniższej zależności:

$$V_{sr} = \frac{\Delta \hspace{.03cm} s}{\Delta \hspace{.03cm} t}$$

gdzie:
Δs  – przemieszczenie ciała,
Δt  – czas, w którym odbywa się przemieszczenie Δs ciała.

Przemieszczenie Δs  ciała możemy zdefiniować jako:

$$\Delta \hspace{.02cm} s = |x_k \hspace{.1cm} – \hspace{.1cm} x_p|$$

gdzie:
x_k  – położenie końcowe ciała,
x_p  – położenie początkowe ciała.

Aby wyznaczyć Δs  dla okresu T  drgań ciała podzielimy krzywą x(t)  na cztery jednakowe obszary tak, jak przedstawiono to na poniższym rysunku:

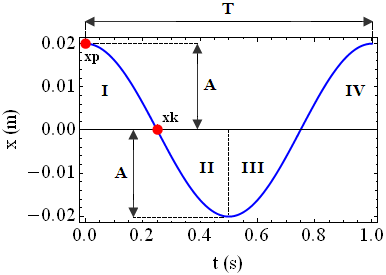
W każdym z czterech zaznaczonych obszarów przemieszczenie ciała zachodzące w czasie t = T/4 wynosi tyle samo. Dla przykładu obliczono przemieszczenie Δx  dla pierwszego obszaru (I):

$$\Delta \hspace{.02cm} x = |x_k \hspace{.1cm} – \hspace{.1cm} x_p| = |0 \hspace{.1cm} – \hspace{.1cm} A| = A$$

Całkowite przemieszczenie Δs  dla wszystkich czterech obszarów (a więc dla całego okresu T  drgań), wynosi:

$$\Delta \hspace{.02cm} s = 4 \hspace{.05cm} \Delta \hspace{.02cm} x = 4 \hspace{.05cm} A$$

Przemieszczenie Δs  zachodzi w czasie Δt = T, zatem średnia prędkość V_sr  wynosi:

$$V_{sr} = \frac{\Delta \hspace{.03cm} s}{\Delta \hspace{.03cm} t} = \frac{4 \hspace{.05cm} A}{T} = \frac{4 \cdot 0,\hspace{-.1cm}02 \hspace{.05cm} \textrm{m}}{1 \hspace{.05cm} \textrm{s}} = 0,\hspace{-.1cm}08 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}}$$