Siła Lorentza – zadanie nr 8

Proton poruszający się z prędkością V  = 10⁵ m/s wpada w jednorodne pole magnetyczne o indukcji B  = 0,4 T pod kątem φ  = 45^o do kierunku wektora indukcji magnetycznej $\vec{B}$. Znajdź promień i skok śruby, po której będzie poruszał się proton. Masa protonu jest znana i wynosi m_p  = 1,6726 ⋅ 10^-27 kg.

(Zadanie ze zbioru: K. Chyła Zbiór prostych zadań z fizyki dla uczniów szkół średnich)

W dotychczasowych zadaniach dotyczących siły Lorentza zajmowaliśmy się przypadkami, w których ruch cząstki naładowanej elektrycznie znajdującej się w zewnętrznym polu magnetycznym, odbywał się po okręgu o promieniu r. W zadaniu Siła Lorentza – zadanie nr 1 wyjaśniliśmy, że ruch cząstki po okręgu jest konsekwencją prostopadłego ułożenia wektorów $\vec{V}$  i  $\vec{B}$, sprawiającego, że wektor prędkości posiada tylko jedną składową: składową prostopadłą do wektora indukcji, styczną do każdego punktu toru poruszającej się cząstki.

W tym zadaniu wektory $\vec{V}$  i  $\vec{B}$ nie są prostopadłe, lecz nachylone do siebie pod kątem φ  = 45^o, w związku z czym wektor prędkości $\vec{V}$ posiada zarówno składową równoległą V_||  oraz składową prostopadłą V_⊥  do wektora $\vec{B}$. Sytuację tą przedstawia poniższy rysunek:

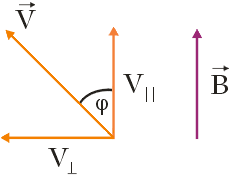
Obecność dwóch składowych wektora prędkości powoduje, że ruch protonu odbywa się po linii śrubowej wokół kierunku wektora indukcji $\vec{B}$. Składowa równoległa V_||  równa $V_{||} = V \hspace{.05cm} \textrm{cos} \hspace{.03cm} \varphi$  określa skok d  linii śrubowej równy drodze przebytej przez proton w kierunku równoległym do wektora $\vec{B}$ podczas jednego okresu ruchu. Składowa prostopadła V_⊥ równa $V_{\perp} = V \hspace{.05cm} \textrm{sin} \hspace{.03cm} \varphi$  określa, z kolei, promień r  linii śrubowej.

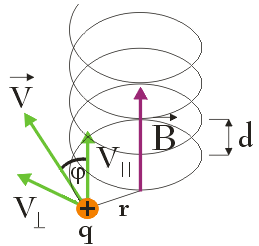
Wielkością szukaną w zadaniu jest promień r  oraz skok d  śruby. Promień r  obliczymy korzystając z poniższego równania (zobacz: Siła Lorentza – zadanie nr 3):

$$r = \frac{\sqrt{\mathstrut 2 \hspace{.05cm} E_k \hspace{.05cm} m}}{|q| \hspace{.03cm} B}$$

Wstawiając w miejsce energii kinetycznej E_k  wyrażenie $E_k = \frac{1}{2} \hspace{.05cm} m_p \hspace{.05cm} V_{\perp}^2$ (w miejsce prędkości protonu wstawiliśmy składową V_⊥, ponieważ to właśnie ta składowa jest styczna do jego toru), a w miejsce q  ładunek protonu równy +e = 1,6021 ⋅ 10^-19 C, otrzymamy:

$$r = \frac{\sqrt{\mathstrut 2 \cdot \frac{1}{2} \hspace{.05cm} m_p \hspace{.05cm} V_{\perp}^2 \hspace{.05cm} m_p}}{e \hspace{.03cm} B} = \frac{\sqrt{\mathstrut m_p^2 \hspace{.05cm} V_{\perp}^2}}{e \hspace{.03cm} B} = \frac{m_p \hspace{.05cm} V \hspace{.05cm} \textrm{sin} \hspace{.05cm} \varphi}{e \hspace{.03cm} B}$$

gdzie m_p  to masa protonu.

Po podstawieniu do powyższego wzoru wartości liczbowych oraz wykonaniu obliczeń, dostaniemy wartość promienia r  równą:

$$r = \frac{1,\hspace{-.1cm}6726 \cdot 10^{-27} \hspace{.05cm} \textrm{kg} \cdot 10^5 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}} \cdot \textrm{sin} \hspace{.03cm} 45^{\textrm{o}}}{1,\hspace{-.1cm}6021 \cdot 10^{-19} \hspace{.05cm} \textrm{C} \cdot 0,\hspace{-.1cm}4 \hspace{.05cm} \textrm{T}} = 1,\hspace{-.1cm}8 \hspace{.05cm} \textrm{mm}$$

Zajmijmy się teraz obliczeniem skoku śruby. Zgodnie z tym co napisaliśmy wyżej, skok d  śruby odpowiada drodze przebytej przez proton w kierunku równoległym do wektora indukcji w czasie jednego okresu T, dlatego:

$$d = s = V_{||} \hspace{.05cm} T$$

Okres T  jest równy (w miejsce częstości kołowej ω  wstawiliśmy wyrażenie ω  = V_⊥ /r ):

$$T = \frac{2 \hspace{.05cm} \pi}{\omega} = \frac{2 \hspace{.05cm} \pi \hspace{.05cm} r}{V_{\perp}} = \frac{2 \hspace{.05cm} \pi \hspace{.05cm} r}{V \hspace{.05cm} \textrm{sin} \hspace{.0cm} \varphi}$$

Korzystając z wyrażenia na promień r  linii śrubowej, mamy:

$$T = \frac{2 \hspace{.05cm} \pi \hspace{.05cm} m_p \hspace{.05cm} V \hspace{.05cm} \textrm{sin} \hspace{.03cm} \varphi}{e \hspace{.05cm} B \hspace{.05cm} V \hspace{.05cm} \textrm{sin} \hspace{.03cm} \varphi} = \frac{2 \hspace{.05cm} \pi \hspace{.05cm} m_p}{e \hspace{.05cm} B}$$

Po wstawieniu powyższego wzoru do równania na skok d  śruby, otrzymamy:

$$d = V_{||} \hspace{.05cm} T = V \hspace{.05cm} \textrm{cos} \hspace{.03cm} \varphi \hspace{.05cm} \frac{2 \hspace{.05cm} \pi \hspace{.05cm} m_p}{e \hspace{.05cm} B}$$

i w efekcie:

$$d = 10^5 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}} \cdot \textrm{cos} \hspace{.03cm} 45^{\textrm{o}} \cdot \frac{2 \cdot 3,\hspace{-.1cm}14 \cdot 1,\hspace{-.1cm}6726 \cdot 10^{-27} \hspace{.05cm} \textrm{kg}}{1,\hspace{-.1cm}6021 \cdot 10^{-19} \hspace{.05cm} \textrm{C} \cdot 0,\hspace{-.1cm}4 \hspace{.05cm} \textrm{T}} = 11,\hspace{-.1cm}6 \hspace{.05cm} \textrm{mm}$$