Siła Lorentza – zadanie nr 7

Oblicz prędkość protonu, który bez odchylenia od swojego pierwotnego kierunku przechodzi przez układ wzajemnie prostopadłych pól: magnetycznego o indukcji B  = 2 T i elektrycznego o natężeniu E  = 1000 V/m. Proton porusza się w kierunku prostopadłym zarówno do wektora $\vec{E}$,  jak i $\vec{B}$.

(Zadanie ze zbioru: K. Chyła Zbiór prostych zadań z fizyki dla uczniów szkół średnich)

Proton, cząstka naładowana dodatnio, przechodząc przez obszar wzajemnie prostopadłych pól: magnetycznego i elektrycznego (tzw. pól skrzyżowanych), doświadcza działania siły elektrycznej $\vec{F}_E$  oraz siły magnetycznej $\vec{F}_B$  (siła Lorentza). Ponieważ proton po przejściu przez obszar tych pól nie ulega odchyleniu od swojego pierwotnego kierunku, zatem siły $\vec{F}_E$  i  $\vec{F}_B$ działające na proton muszą się równoważyć (muszą mieć jednakową wartość).

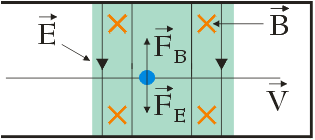
Siła związana z polem elektrycznym jest równa F_E  = |q| E, z kolei siła związana z polem magnetycznym – F_B  = |q| V B. Ładunek elektryczny protonu wynosi +e. Po przyrównaniu stronami tych dwóch sił, dostaniemy:

$$e \hspace{.05cm} E = e \hspace{.05cm} V \hspace{.05cm} B$$

Po skróceniu i przekształceniu powyższego wyrażenia względem prędkości V, otrzymamy:

$$V = \frac{E}{B}$$

i w efekcie:

$$V = \frac{1000 \hspace{.05cm} \tfrac{\textrm{V}}{\textrm{m}}}{2 \hspace{.05cm} \textrm{T}} = 500 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}}$$