Rzut ukośny

Rzut ukośny to przykład ruchu ciała odbywającego się w dwóch wymiarach przestrzeni: w płaszczyźnie poziomej x  oraz w płaszczyźnie pionowej y. Jeżeli pominiemy opór powietrza, wówczas, jak się za chwilę przekonasz, ruch ciała w kierunku poziomym odbywa się ze stałą prędkością V_x  = V_0x  (przyspieszenie w tym kierunku jest równe a  = 0 m/s²), z kolei ruch w kierunku pionowym – ze zmienną prędkością V_y  (ciało porusza się w pionie ze stałym przyspieszeniem ziemskim $\vec{g}$). Dla lepszego zobrazowania opisanej sytuacji stworzono poniższy rysunek:

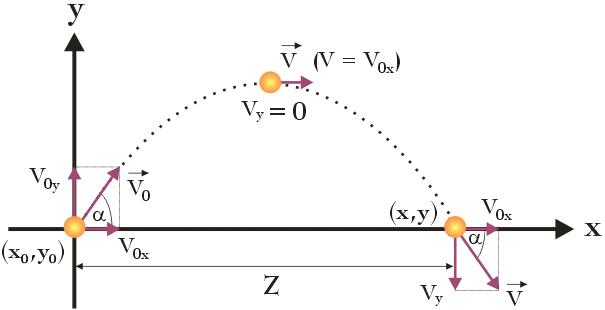
Korzystając z zapisu wektorowego, prędkość początkową ciała $\vec{V}_0$  możemy zapisać jako:

$$\vec{V}_0 = V_{0x} \hspace{.05cm} \hat{i} + V_{0y} \hspace{.05cm} \hat{j}$$

gdzie $\hat{i}$  i  $\hat{j}$ to wektory jednostkowe (wektory o długości równej 1 skierowane odpowiednio wzdłuż osi x  oraz y).

Zgodnie z rysunkiem składowa V_0x  wynosi:

$$V_{0x} = V_0 \hspace{.05cm} \textrm{cos} \hspace{.05cm} \alpha$$

a składowa V_0y :

$$V_{0y} = V_0 \hspace{.05cm} \textrm{sin} \hspace{.05cm} \alpha$$

Ruch ciała w kierunku poziomym

Aby opisać ruch ciała w kierunku poziomym i pionowym skorzystamy ze wzorów na prędkość i drogę w ruchu jednostajnie przyspieszonym. Przemieszczenie ciała w poziomie wynosi:

$$x \hspace{.15cm} – \hspace{.05cm} x_0 = V_{0x} \hspace{.05cm} t + \tfrac{1}{2} \hspace{.05cm} a \hspace{.05cm} t^2$$

gdzie:
x₀  – położenie początkowe ciała,
x  – położenie końcowe ciała.

Przyspieszenie ciała w kierunku poziomym wynosi a  = 0 m/s², dlatego:

$$x \hspace{.15cm} – \hspace{.05cm} x_0 = V_{0x} \hspace{.05cm} t = V_0 \hspace{.05cm} \textrm{cos} \hspace{.05cm} \alpha \hspace{.05cm} t$$

Prędkość ciała wzdłuż osi x, zgodnie z tym co napisaliśmy wcześniej, przyjmuje stałą wartość równą:

$$V_x = V_{0x} + a \hspace{.05cm} t = V_{0x} = V_0 \hspace{.05cm} \textrm{cos} \hspace{.05cm} \alpha$$

Ruch ciała w kierunku pionowym

Ruch ciała w pionie odbywa się ze stałym przyspieszeniem ziemskim $\vec{g}$, w związku z czym przemieszczenie ciała w tym kierunku wynosi ($\vec{g}$  jest skierowane w dół, dlatego a  = – g ):

$$y \hspace{.15cm} – \hspace{.05cm} y_0 = V_{0y} \hspace{.05cm} t + \tfrac{1}{2} \hspace{.05cm} a \hspace{.05cm} t^2 = V_0 \hspace{.05cm} \textrm{sin} \hspace{.05cm} \alpha \hspace{.05cm} t \hspace{.15cm} – \hspace{.05cm} \tfrac{1}{2} \hspace{.05cm} g \hspace{.05cm} t^2$$

Prędkość ciała wzdłuż osi y  wynosi z kolei:

$$V_y = V_{0y} + a \hspace{.05cm} t = V_0 \hspace{.05cm} \textrm{sin} \hspace{.05cm} \alpha \hspace{.15cm} – \hspace{.05cm} g \hspace{.05cm} t$$

Ruch w kierunku pionowym odpowiada spadkowi swobodnemu ciała.

Zasięg rzutu ukośnego

Wielkością charakterystyczną dla rzutu ukośnego jest wielkość fizyczna nazywana zasięgiem poziomym rzutu Z. Zasięg rzutu to odległość jaką przebywa ciało w poziomie od chwili jego wyrzutu do chwili powrotu na wysokość, z której zostało wyrzucone. Wzór pozwalający obliczyć zasięg Z  przedstawia się następująco:

$$Z = \frac{V_0^2}{g} \hspace{.05cm} \textrm{sin} \hspace{.05cm} 2 \hspace{.05cm} \alpha$$

Zauważ, że zasięg rzutu Z  przyjmuje największą wartość wtedy, gdy wielkość sin (2 α ) = 1, co oznacza, że α  = 45^o (2 α = 90^o  →  α = 45^o).

Wyprowadzenie powyższego wzoru znajdziesz tutaj: Zasięg rzutu ukośnego – wyprowadzenie wzoru.

Rzut ukośny – równanie toru

Gdy przekształcimy równanie opisujące ruch ciała w kierunku poziomym względem czasu t :

$$x \hspace{.15cm} – \hspace{.05cm} x_0 = V_0 \hspace{.05cm} \textrm{cos} \hspace{.05cm} \alpha \hspace{.05cm} t \hspace{1cm} \longrightarrow \hspace{1cm} t = \frac{x \hspace{.15cm} – \hspace{.05cm} x_0}{V_0 \hspace{.05cm} \textrm{cos} \hspace{.05cm} \alpha}$$

i podstawimy je do wyrażenia na przemieszczenie ciała w kierunku pionowym:

$$y \hspace{.15cm} – \hspace{.05cm} y_0 = V_0 \hspace{.05cm} \textrm{sin} \hspace{.05cm} \alpha \hspace{.05cm} t \hspace{.15cm} – \hspace{.05cm} \tfrac{1}{2} \hspace{.05cm} g \hspace{.05cm} t^2 = V_0 \hspace{.05cm} \textrm{sin} \hspace{.05cm} \alpha \cdot \frac{x \hspace{.15cm} – \hspace{.05cm} x_0 }{V_0 \hspace{.05cm} \textrm{cos} \hspace{.05cm} \alpha} \hspace{.15cm} – \hspace{.05cm} \tfrac{1}{2} \hspace{.05cm} g \hspace{.05cm} \frac{\left( x \hspace{.15cm} – \hspace{.05cm} x_0 \right)^2}{V_0^2 \hspace{.05cm} \textrm{cos}^2 \hspace{.05cm} \alpha}$$

otrzymamy, przy założeniu, że x₀  = y₀  = 0 m, równanie toru ciała w rzucie ukośnym:

$$y = \textrm{tg} \hspace{.05cm} \alpha \hspace{.05cm} x \hspace{.15cm} – \hspace{.05cm} \frac{g}{2 \hspace{.05cm} V_0^2 \hspace{.05cm} \textrm{cos}^2 \hspace{.05cm} \alpha} \hspace{.05cm} x^2$$

Równanie toru w rzucie ukośnym jest równaniem paraboli, a więc tor ciała, zgodnie z powyższym rysunkiem, jest torem parabolicznym.

Inne przydatne wzory

• maksymalna wysokość jaką może osiągnąć ciało:

$$y_{max} = \frac{V_0^2 \hspace{.05cm} \textrm{sin}^2 \alpha}{2 \hspace{.05cm} g}$$

• czas lotu ciała (od chwili wyrzutu do chwili upadku na wysokość, z której ciało zostało wyrzucone):

$$t_{lot} = \frac{2 \hspace{.05cm} V_0 \hspace{.05cm} \textrm{sin} \hspace{.05cm} \alpha}{g}$$

• czas wznoszenia ciała do osiągnięcia wysokości y_max :

$$t_{max} = \frac{V_0 \hspace{.05cm} \textrm{sin} \hspace{.05cm} \alpha}{g}$$