Ruch jednostajnie przyspieszony

Gdy prędkość ciała ulega zmianie w czasie mówimy, że ciało to doznaje przyspieszenia. Gdybyśmy chcieli dowiedzieć się ile wynosi średnia wartość przyspieszenia a_sr  ciała poruszającego się wzdłuż pewnej osi (np. osi x ), skorzystalibyśmy wówczas z poniższego wzoru:

$$a_{sr} = \frac{\Delta \hspace{.03cm} V}{\Delta \hspace{.03cm} t} = \frac{V \hspace{.1cm} – \hspace{.1cm} V_0}{t \hspace{.1cm} – \hspace{.1cm} t_0}$$

gdzie:
V  – prędkość ciała w chwili t,
V₀  – prędkość ciała w chwili t₀.

Przyspieszenie

Ruch ciała odbywający się z pewnym (niezerowym) przyspieszeniem nazywamy ruchem przyspieszonym. Szczególnym przypadkiem tego rodzaju ruchu jest ruch jednostajnie przyspieszony, w którym ciało porusza się ze stałą (niezmienną) wartością przyspieszenia (wyraz jednostajnie przyspieszony oznacza właśnie bez zmiany przyspieszenia).

Ponieważ przyspieszenie ciała w ruchu jednostajnie przyspieszonym przyjmuje stałą wartość (a  = constans), przyspieszenie średnie a_sr  (w tym ruchu) jest równe wartości przyspieszenia a  ciała:

$$a = a_{sr} = \frac{\Delta \hspace{.03cm} V}{\Delta \hspace{.03cm} t} = \frac{V \hspace{.1cm} – \hspace{.1cm} V_0}{t \hspace{.1cm} – \hspace{.1cm} t_0}$$

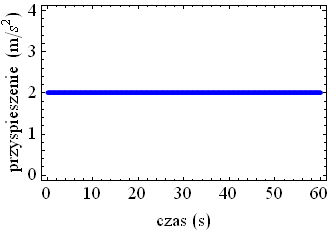
Poniższy rysunek przedstawia zależność przyspieszenia a  ciała w funkcji czasu w ruchu jednostajnie przyspieszonym. Zwróć uwagę, że podobnie jak w przypadku wykresu prędkości od czasu w ruchu jednostajnym prostoliniowym, wykresem zależności a (t ) jest pozioma linia opisana funkcją stałą postaci y  = a.

Zakładając, że ciało w chwili t₀  = 0 s posiada prędkość V₀, dostaniemy:

$$a = \frac{V \hspace{.1cm} – \hspace{.1cm} V_0}{t}$$

Prędkość w ruchu jednostajnie przyspieszonym

Przekształcając powyższy wzór względem V  otrzymamy ogólną zależność opisującą prędkość ciała w funkcji czasu w ruchu jednostajnie przyspieszonym:

$$V = a \hspace{.05cm} t + V_0$$

Zależność opisaną powyższym wyrażeniem przedstawia poniższy rysunek. Zauważ, że prędkość ciała w ruchu jednostajnie przyspieszonym zmienia się liniowo w funkcji czasu, w związku z czym jej wykresem, podobnie jak wykresem położenia ciała w ruchu jednostajnym prostoliniowym, jest prosta postaci y  = ax  + b.

Aby wyznaczyć ogólną zależność opisującą położenie ciała w funkcji czasu w ruchu jednostajnie przyspieszonym zapiszmy na początek wyrażenie na średnią prędkość ciała:

$$V_{sr} = \frac{\Delta \hspace{.05cm} x}{\Delta \hspace{.05cm} t} = \frac{x \hspace{.1cm} – \hspace{.1cm} x_0}{t \hspace{.1cm} – \hspace{.1cm} t_0} = \frac{x \hspace{.1cm} – \hspace{.1cm} x_0}{t}$$

gdzie:
x  – położenie ciała w chwili t,
x₀  – położenie ciała w chwili t₀  = 0 s (t₀  = 0 s, ponieważ takie samo założenie przyjęliśmy we wzorze na przyspieszenie a).

Przekształcając powyższy wzór względem x, dostaniemy:

$$x = V_{sr} \hspace{.1cm} t + x_0$$

Jak napisaliśmy wyżej, prędkość ciała w ruchu jednostajnie przyspieszonym zmienia się liniowo z czasem, w związku z czym średnia prędkość ciała (w tym ruchu) w pewnym przedziale czasu np. od chwili t₀  do chwili t, jest równa średniej arytmetycznej prędkości V₀  ciała na początku ruchu (w chwili t₀ ) oraz prędkości V  ciała na końcu ruchu (w chwili t ):

$$V_{sr} = \frac{V_0 + V}{2}$$

Droga w ruchu jednostajnie przyspieszonym

Gdy do wzoru na V_sr  w miejsce prędkości V  wstawimy wyrażenie V  = at  + V₀, otrzymamy:

$$V_{sr} = \frac{V_0 + a \hspace{.05cm} t + V_0}{2} = \frac{a \hspace{.05cm} t + 2 \hspace{.05cm} V_0}{2} = \frac{a \hspace{.05cm} t}{2} + V_0$$

Po podstawieniu powyższej zależności do wzoru  $x = V_{sr} \hspace{.1cm} t + x_0$  otrzymamy ogólne wyrażenie opisujące położenie ciała w funkcji czasu w ruchu jednostajnie przyspieszonym:

$$x = \left( \frac{a \hspace{.05cm} t}{2} + V_0 \right) t + x_0 = \tfrac{1}{2} \hspace{.05cm} a \hspace{.05cm} t^2 + V_0 \hspace{.05cm} t + x_0$$

Gdy w miejsce x  oraz x₀  wstawimy następnie s  oraz s₀, dostaniemy:

$$s = \tfrac{1}{2} \hspace{.05cm} a \hspace{.05cm} t^2 + V_0 \hspace{.05cm} t + s_0$$

Zgodnie z dwoma powyższymi wzorami położenie ciała w ruchu jednostajnie przyspieszonym zmienia się kwadratowo z czasem, co przedstawia poniższy rysunek: