Ruch jednostajny prostoliniowy

Ruch jednostajny prostoliniowy to ruch, podczas trwania którego ciało porusza się ze stałą prędkością po linii prostej (słowo jednostajny oznacza bez zmian – w tym przypadku bez zmiany prędkości). Prędkość w ruchu jednostajnym prostoliniowym zapisana w postaci wektorowej wyraża się poniższym wzorem:

$$\vec{V} = \frac{\vec{r}}{t} = \frac{r_x \hspace{.05cm} \hat{i} + r_y \hspace{.05cm} \hat{j} + r_z \hspace{.05cm} \hat{k}}{t}$$

gdzie:
r_x, r_y  i r_z  – składowe wektora położenia $\vec{r}$,
$\hat{i}$, $\hat{j}$, $\hat{k}$  – wektory jednostkowe (wektory o długości jeden).

Prędkość w ruchu jednostajnym prostoliniowym

Często jednak, zwłaszcza rozwiązując zadania, będziemy korzystali z nieco uproszczonego wzoru zapisywanego w postaci skalarnej. Wzór ten uwzględnia zależność prędkości V  tylko od jednej składowej przestrzennej, np. x, oznaczanej małą literą s :

$$V = \frac{s}{t}$$

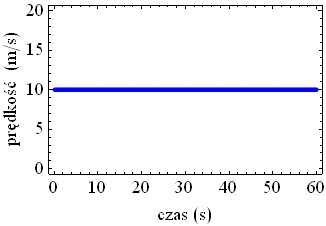
Poniższy rysunek przedstawia zależność prędkości w funkcji czasu w ruchu jednostajnym prostoliniowym dla ciała poruszającego się z prędkością V  = 10 m/s. Zależność ta opisana jest przez funkcję stałą postaci y  = a , gdzie a  jest dowolną liczbą. Zauważ, że zgodnie z tym co napisaliśmy wyżej, prędkość ciała przyjmuje stałą wartość podczas trwania jego ruchu.

Prędkość średnia

Kolejną wielkością fizyczną informującą o tym jak szybko porusza się ciało w ruchu jednostajnym prostoliniowym jest prędkość średnia. Prędkość tą definiujemy jako stosunek przemieszczenia ciała odbywającego się w pewnym przedziale czasu, do wartości tego przedziału czasu i zapisujemy w poniższej formie:

– w postaci wektorowej:

$$\vec{V}_{sr} = \frac{\Delta \hspace{.03cm} \vec{r}}{\Delta \hspace{.03cm} t} = \frac{\Delta \hspace{.03cm} r_x}{\Delta \hspace{.03cm} t} \hat{i} + \frac{\Delta \hspace{.03cm} r_y}{\Delta \hspace{.03cm} t} \hat{j} + \frac{\Delta \hspace{.03cm} r_z}{\Delta \hspace{.03cm} t} \hat{k}$$

– w postaci skalarnej:

$$V_{sr} = \frac{\Delta \hspace{.03cm} s}{\Delta \hspace{.03cm} t} = \frac{s \hspace{.1cm} – \hspace{.1cm} s_0}{t \hspace{.1cm} – \hspace{.1cm} t_0}$$

gdzie:
s  – położenie ciała w chwili t,
s₀  – położenie ciała w chwili t₀.

Średnią wartość prędkości w ruchu jednostajnym prostoliniowym możemy także łatwo wyznaczyć na podstawie wykresu przedstawiającego zależność położenia ciała w funkcji czasu w tymże właśnie ruchu (zobacz poniższy rysunek). W tym przypadku prędkość średnia ciała równa jest współczynnikowi kierunkowemu prostej y  = ax  + b  opisującej zależność s  = f(t ) w ruchu jednostajnym prostoliniowym (współczynnik kierunkowy odpowiada za nachylenie, w naszym przypadku – niebieskiej, krzywej). Aby wyznaczyć współczynnik kierunkowy prostej wystarczy dla dwóch dowolnych punktów na poniższym wykresie odczytać ich współrzędną położenia oraz czasu i następnie podstawić odczytane wartości liczbowe do powyższego wzoru na prędkość średnią ciała).

Droga w ruchu jednostajnym prostoliniowym

Podstawiając odpowiednie wielkości fizyczne do zależności funkcyjnej y  = ax  + b  dostaniemy ogólne wyrażenie opisujące położenie ciała w funkcji czasu w ruchu jednostajnym prostoliniowym:

$$s = V \hspace{.05cm} t + s_0$$

gdzie w miejsce y  wstawiliśmy s, czyli położenie ciała w chwili t, w miejsce a  – prędkość V  ciała, w miejsce x  – czas t, z kolei w miejsce wyrazu wolnego b  – wielkość s₀  odpowiadającą położeniu ciała w chwili t₀.

Gdy w chwili t₀  położenie ciała s₀  = 0 m, wówczas powyższe wyrażenie sprowadza się do następującej postaci:

$$s = V \hspace{.05cm} t$$