Prawo powszechnego ciążenia – zadanie nr 2

Satelita geostacjonarny ma postać kulistego balonu o średnicy 20 m i masie 50 kg. W pewnej chwili meteoroid o masie 10 kg przelatuje w odległości 5 m od powierzchni satelity. Oblicz wartość siły grawitacji, jaką działa satelita na meteoroid w momencie ich największego zbliżenia. Stała grawitacji G  = 6,67 ∙ 10^-11 N ∙ m²/kg².

Zacznijmy od zapisania wyrażenia opisującego wartość siły F, z jaką satelita oraz meteoroid oddziałują na siebie wzajemnie (zobacz: Prawo powszechnego ciążenia):

$$F = G \hspace{.05cm} \frac{m_s \hspace{.1cm} m_m}{r^2}$$

gdzie:
m_s  – masa satelity,
m_m  – masa meteoroidu.

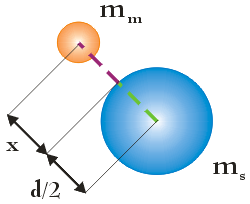
Zgodnie z powyższym wzorem obliczenie szukanej wartości siły F  wymaga od nas znajomości mas obydwu obiektów oraz odległości r  pomiędzy ich środkami. Masy m_s  i m_m  podano w treści zadania. Odległość r  nie jest znana. Możemy ją jednak z łatwością wyznaczyć. Wiemy ile wynosi dystans x  dzielący środek meteoroidu od powierzchni satelity oraz znamy średnicę d  satelity (zobacz rysunek). Ponieważ, jak napisaliśmy wyżej, r  jest odległością między środkiem satelity a meteoroidu, w związku z czym:

$$r = x + \frac{d}{2} = 5 \hspace{.05cm} \textrm{m} + \frac{20 \hspace{.05cm} \textrm{m}}{2} = 15 \hspace{.05cm} \textrm{m}$$

Znając wartość r  możemy obliczyć wartość siły wzajemnego przyciągania się satelity oraz meteoroidu:

$$F = 6,\hspace{-.1cm}67 \cdot 10^{-11} \hspace{.05cm} \tfrac{\textrm{N} \cdot \textrm{m}^2}{\textrm{kg}^2} \cdot \frac{50 \hspace{.05cm} \textrm{kg} \cdot 10 \hspace{.05cm} \textrm{kg}}{\left( 15 \hspace{.05cm} \textrm{m} \right)^2} = 14,\hspace{-.1cm}8 \cdot 10^{-11} \hspace{.05cm} \textrm{N} = 148 \hspace{.05cm} \textrm{pN}$$