Płyny w spoczynku. Ciśnienie hydrostatyczne – zadanie nr 3

W naczyniu w kształcie litery U znajdują się dwie nie mieszające się ze sobą ciecze znajdujące się w równowadze statycznej (zobacz: rysunek). W prawym ramieniu naczynia znajduje się woda o gęstości ρ_w  = 1000 kg/m³, a w lewym – substancja o nieznanej gęstości ρ. Oblicz gęstość tej substancji wiedząc, że wysokości słupów obydwu cieczy wynoszą: l  = 15 cm, d  = 18 cm.

Zgodnie z poniższym wzorem wartość ciśnienia hydrostatycznego na pewnej głębokości h  pod powierzchnią cieczy o gęstości ρ  wynosi:

$$p = p_0 + \rho \hspace{.05cm} g \hspace{.05cm} h$$

gdzie:
p₀ – ciśnienie atmosferyczne działające na powierzchnię cieczy,
g  – przyspieszenie ziemskie.

Zauważ, że wartość ciśnienia p  jest tym większa im większa jest gęstość ρ  cieczy oraz głębokość h  pod jej powierzchnią.

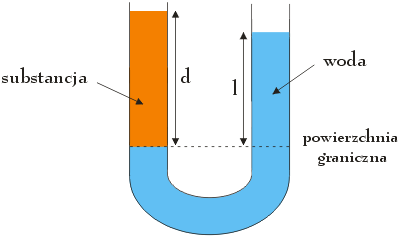
Jak wynika z treści zadania obydwie ciecze znajdują się w stanie równowagi statycznej, co oznacza że wartość ciśnienia w punktach znajdujących się na jednakowym poziomie musi przyjmować takie same wartości (nawet wtedy, gdy punkty te znajdują się w różnych, lecz połączonych ze sobą ramionach naczynia). Korzystając z tego faktu możemy stwierdzić, że ciśnienie wywierane przez nieznaną substancję oraz wodę na poziomie powierzchni granicznej musi mieć jednakową wartość (domyślamy się, że skoro wysokość słupów obydwu cieczy nie jest jednakowa, ciecze te muszą posiadać różną gęstość). W związku z tym dla jednej oraz drugiej cieczy prawdziwe będą poniższe relacje:

– dla nieznanej substancji:

$$p = p_0 + \rho \hspace{.05cm} g \hspace{.05cm} d$$

– dla wody:

$$p_w = p_0 + \rho_w \hspace{.05cm} g \hspace{.05cm} l$$

gdzie d  i l  to odpowiednio wysokość słupa nieznanej substancji (lewe ramię naczynia) oraz wody (prawe ramię naczynia).

Po przyrównaniu stronami równań na p  i p_w, dostaniemy:

$$p = p_w \hspace{1cm} \longrightarrow \hspace{1cm} p_0 + \rho \hspace{.05cm} g \hspace{.05cm} d = p_0 + \rho_w \hspace{.05cm} g \hspace{.05cm} l \hspace{1cm} \longrightarrow \hspace{1cm} \rho \hspace{.05cm} d = \rho_w \hspace{.05cm} l$$

skąd po przekształceniu powyższej zależności względem gęstości ρ, podstawieniu wartości liczbowych oraz wykonaniu obliczeń, otrzymamy:

$$\rho = \rho_w \hspace{.05cm} \frac{l}{d} = 1000 \hspace{.05cm} \tfrac{\textrm{kg}}{\textrm{m}^3} \cdot \frac{15 \hspace{.05cm} \textrm{cm}}{18 \hspace{.05cm} \textrm{cm}} = 833 \hspace{.05cm} \tfrac{\textrm{kg}}{\textrm{m}^3}$$