Płyny w spoczynku. Ciśnienie hydrostatyczne

Badaniem płynów znajdujących się w stanie spoczynku zajmują się działy mechaniki płynów nazywane hydrostatyką oraz aerostatyką. Pierwszy z wymienionych działów dotyczy cieczy, drugi z nich – gazów. Najprostszym przykładem płynu pozostającego w stanie spoczynku, który znasz z pewnością z własnego doświadczenia, jest woda wypełniająca częściowo lub całkowicie objętość szklanki lub innego naczynia. Być może wiesz również, że wraz ze wzrostem głębokości pod powierzchnią wody, wartość ciśnienia hydrostatycznego (ciśnienie wywierane przez pozostający w spoczynku płyn) wzrasta, z kolei w przypadku osiągania coraz to wyższych wysokości nad poziomem morza, np. podczas wspinaczki górskiej, wartość ciśnienia hydrostatycznego ulega stopniowemu zmniejszaniu. W artykule tym zajmiemy się wyprowadzeniem zależności pozwalającej obliczać wartość tego rodzaju ciśnienia jako funkcję głębokości pod powierzchnią wody lub wysokości nad poziomem morza.

Ciśnienie hydrostatyczne – wyprowadzenie ogólnej zależności

Wyobraźmy sobie, że w pewnym prostokątnym naczyniu, częściowo wypełnionym wodą, wybraliśmy pewną objętość wody zawartą w prostopadłościanie, tak jak przedstawia to poniższy rysunek. Obydwie (górna oraz dolna) podstawy prostopadłościanu, każda o polu powierzchni równym S, znajdują się na różnej głębokości pod powierzchnią wody, w związku z czym ciśnienie wywierane na ich powierzchnię przez otaczającą je wodę przyjmuje różne wartości: p₁ (górna podstawa) oraz p₂ (dolna podstawa).

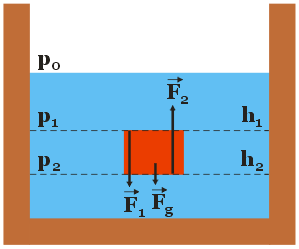
Woda zawarta w prostopadłościanie znajduje się w stanie spoczynku, a zatem wszystkie siły, które na nią działają równoważą się. Korzystając z tego faktu możemy zapisać następującą relację:

$$F_2 = F_1 + F_g$$

gdzie:
F₂ – siła działająca na dolną podstawę prostopadłościanu ze strony wody znajdującej się pod jej powierzchnią,
F₁ – siła działająca na górną podstawę prostopadłościanu ze strony wody znajdującej się nad jej powierzchnią,
F_g – siła ciężkości działająca na prostopadłościan równa m ⋅ g, gdzie m  to masa wody zawarta w prostopadłościanie, a g  to przyspieszenie ziemskie.

Siły F₁ i F₂ działające na górną i dolną podstawę prostopadłościanu, możemy powiązać z ciśnieniem p₁ i p₂, wywieranym przez wodę na każdą z tych powierzchni, za pomocą poniższych równań:

$$F_1 = p_1 \hspace{.05cm} S \hspace{1cm} , \hspace{1cm} F_2 = p_2 \hspace{.05cm} S$$

Masę wody m  stanowiącą rozważany prostopadłościan możemy wyrazić jako iloczyn gęstości ρ  oraz objętości V  prostopadłościanu, która, zgodnie z definicją, wyrażona jest poprzez iloczyn pola powierzchni S  jego podstawy oraz wysokości h₁ – h₂ (zobacz: rysunek).

Korzystając z powyższych równań definiujących siły działające na prostopadłościan i podstawiając je do wzoru opisującego równowagę sił, otrzymamy ogólne wyrażenie pozwalające obliczyć wartość ciśnienia hydrostatycznego wywieranego przez ciecz albo atmosferę:

$$p_2 \hspace{.05cm} S = p_1 \hspace{.05cm} S + \rho \hspace{.05cm} g \hspace{.05cm} S \left( h_1 \hspace{.1cm} – \hspace{.1cm} h_2 \right)$$

Po podzieleniu obydwu stron powyższego równania przez pole powierzchni S, otrzymamy:

$$p_2 = p_1 + \rho \hspace{.05cm} g \left( h_1 \hspace{.1cm} – \hspace{.1cm} h_2 \right)$$

Ciśnienie cieczy na głębokości h

Jeżeli interesuje nas obliczenie wartości ciśnienia p  na określonej głębokości h  pod powierzchnią cieczy, konieczne staje się wprowadzenie pewnych oznaczeń oraz podstawień do powyższego wzoru. W tym celu ponownie wybieramy pewną objętość V  wody zawartą w prostopadłościanie, którego górna podstawa tym razem znajduje się na powierzchni cieczy – h₁ = 0, a dolna – na głębokości h  pod jej powierzchnią – h₂ = –h. Ciśnienie na powierzchni cieczy odpowiada ciśnieniu atmosferycznemu – p₁ = p₀, z kolei ciśnienie na głębokości –h  wynosi p₂ = p. Po podstawieniu tych wielkości do powyższego wyrażenia opisującego ciśnienie hydrostatyczne, uzyskamy równanie pozwalające obliczyć wartość ciśnienia na pewnej głębokości pod powierzchnią cieczy:

$$p = p_0 + \rho \hspace{.05cm} g \hspace{.05cm} h$$

gdzie ρ  jest gęstością cieczy, w tym przypadku wody, wypełniającej objętość zbiornika.

Ciśnienie atmosferyczne na wysokości h

Podobnie jak w powyższym przypadku, obliczenie wartości ciśnienia atmosferycznego na określonej wysokości h  nad poziomem morza, wymaga wprowadzenia pewnych oznaczeń oraz podstawień. Wybierzmy więc pewną objętość powietrza ograniczoną prostopadłościanem, dla którego poszczególne wielkości h  i p  przedstawiają się następująco: h₁ = 0, h₂ = h, p₁ = 0 oraz p₂ = p.

Podstawienie tych wielkości do ogólnego wyrażenia opisującego ciśnienie hydrostatyczne pozwoli nam otrzymać wzór, za pomocą którego będziemy w stanie obliczyć wartość ciśnienia atmosferycznego na określonej wysokości h  nad poziomem morza:

$$p = p_0 \hspace{.1cm} – \hspace{.1cm} \rho \hspace{.05cm} g \hspace{.05cm} h$$

gdzie ρ  jest gęstością powietrza.

Ciśnienie p występujące w dwóch powyższych wzorach nazywa się ciśnieniem bezwzględnym albo pełnym, ponieważ na wartość tego ciśnienia składają się dwa przyczynki: jeden – związany z ciśnieniem atmosferycznym p₀, a więc związany z naciskiem powietrza, drugi – związany z ciśnieniem (naciskiem) cieczy/gazu, równym ρgh, położonego powyżej/poniżej pewnego poziomu oznaczonego jako h.