Prawo Pascala. Prasa hydrauliczna

Ciśnienie to skalarna wielkość fizyczna, której jednostką w układzie SI, jak pewnie doskonale pamiętasz, jest paskal (ozn. Pa), nazwany tak na cześć francuskiego fizyka i matematyka Blaise Pascala (1623-1662). Pascal podczas swojej pracy naukowej wsławił się m.in. sformułowaniem w 1652 roku fundamentalnego prawa mechaniki płynów znanego powszechnie prawem Pascala, które mówi, że:

Prawo Pascala – definicja

Inną wersją prawa Pascala, z jaką możesz się spotkać jest:

Nie wiem czy wiesz, ale co najmniej kilkukrotnie w ciągu każdego dnia świadomie, bądź nie, wykorzystujesz prawo Pascala, aby np. wycisnąć pewną ilość pasty do zębów z tubki. Innym przykładem wykorzystującym prawo Pascala jest tzw. metoda Heimlicha stosowana w celu wypchnięcia ciała obcego z gardła osoby, która uległa zadławieniu, czy też prasa hydrauliczna (słowo hydrauliczny oznacza działający przy użyciu płynu), której poświęcimy obecnie trochę więcej uwagi.

Prawo Pascala, a prasa hydrauliczna

Prasa hydrauliczna to bardzo przydatne urządzenie, ponieważ, jak za chwilę wykażemy, umożliwia działanie siłą o mniejszej wartości na dłuższej drodze zamiast działania większą siłą na krótszej drodze, pozwalając tym samym na podnoszenie bardzo ciężkich przedmiotów przy użyciu znacznie mniejszej siły.

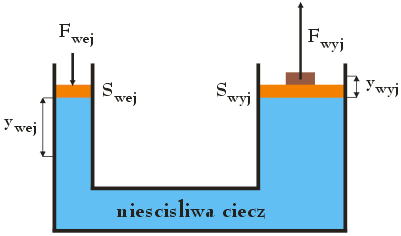
Powyższy rysunek w sposób schematyczny przedstawia budowę prasy hydraulicznej składającej się z dwóch tłoków o dwóch różnych polach powierzchni S_wej  i S_wyj  oraz nieściśliwej cieczy (cieczy o stałej gęstości) wypełniającej objętość pomiędzy tłokami. Wyobraźmy sobie, że na tłok o powierzchni S_wej  działamy siłą o stałej wartości równej F_wej, powodującą przemieszczenie tłoka o odcinek y_wej. Dzięki temu, że ciecz jest nieściśliwa, na tłok w prawym ramieniu prasy o polu S_wyj  działa siła o wartości F_wyj  skierowana pionowo w górę, która powoduje przemieszczenie przedmiotu (brązowy prostokąt) o odcinek y_wyj. Zauważ, że aby układ znajdował się w stanie równowagi statycznej siła F_wyj  musi być równoważona przez siłę ciężkości działającą na przedmiot. Korzystając z wyrażenia definiującego ciśnienie płynów oraz z prawa Pascala możemy powiązać siły F_wej  i F_wyj  działające na tłoki z ich powierzchniami S_wej  i S_wyj  zapisując zmianę ciśnienia cieczy Δp  jako:

$$\Delta \hspace{.03cm} p = \frac{F_{wej}}{S_{wej}} = \frac{F_{wyj}}{S_{wyj}}$$

skąd po przekształceniu otrzymamy wyrażenie na siłę działającą na podnoszony przedmiot:

$$F_{wyj} = \frac{F_{wej} \hspace{.1cm} S_{wyj}}{S_{wej}}$$

Prasa hydrauliczna – podnoszenie ciężkich przedmiotów przy użyciu niewielkiej siły

Z powyższego równania wynika bardzo cenna informacja: wartość siły F_wyj  jest większa od siły F_wej  tylko wtedy, gdy pole powierzchni S_wyj  tłoka w prawym ramieniu prasy jest większe od pola powierzchni S_wej  tłoka w lewym ramieniu prasy, czyli dokładnie tak jak przedstawiono to na rysunku. W przeciwnym razie nie osiągniemy zamierzonego efektu tzn. aby podnieść przedmiot o znacznej masie będziemy musieli włożyć znacznie więcej wysiłku, który oczywiście nie będzie nam gwarantował powodzenia takiego przedsięwzięcia.

Wiedząc ile wynosi wartość siły F_wyj  obliczymy następnie pracę wykonaną przez tą siłę przy podniesieniu przedmiotu o odcinek y_wyj. W tym celu ponownie skorzystamy z faktu, że ciecz wypełniająca objętość ograniczoną powierzchnią tłoków jest cieczą nieściśliwą, co oznacza, że konsekwencją działania siły F_wej  będzie przemieszczenie się przy obydwu tłokach jednakowych objętości V  cieczy równych:

$$V = S_{wej} \hspace{.1cm} y_{wej} = S_{wyj} \hspace{.1cm} y_{wyj}$$

Przekształcając powyższe wyrażenie uzyskamy wzór opisujący przemieszczenie y_wyj  dużego tłoka:

$$y_{wyj} = \frac{S_{wej} \hspace{.1cm} y_{wej}}{S_{wyj}}$$

Zauważ, że jeżeli S_wyj  > S_wej, to przemieszczenie tłoka w prawym ramieniu prasy będzie mniejsze, niż tłoka w lewym ramieniu, co jest oczywiście zjawiskiem pożądanym i zgodnym z zamieszczonym wyżej rysunkiem.

Praca wykonana przez siłę wyjściową

Przystąpmy teraz do obliczenia pracy wykonanej przez siłę F_wyj :

$$W = F_{wyj} \hspace{.1cm} y_{wyj} = \left( \frac{F_{wej} \hspace{.1cm} S_{wyj}}{S_{wej}} \right) \cdot \left( \frac{y_{wej} \hspace{.1cm} S_{wej}}{S_{wyj}} \right) = F_{wej} \hspace{.1cm} y_{wej}$$

W ten sposób dowiedliśmy, że praca wykonana nad tłokiem w lewym ramieniu prasy przez siłę F_wej  jest równa pracy wykonanej przez tłok w prawym ramieniu prasy przy podnoszeniu przedmiotu. Ta właściwość prasy hydraulicznej jest niezwykle istotna, ponieważ jak napisaliśmy na początku tego artykułu, pozwala uzyskać dużo większą siłę, niż ta, którą musielibyśmy przyłożyć, aby podnieść samochód, czy też inny przedmiot o znacznej masie.