Ciśnienie płynów
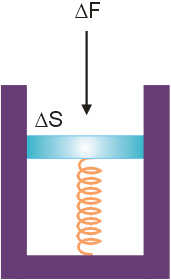
Aby wyznaczyć ciśnienie płynu w dowolnym jego punkcie możemy posłużyć się prostym przyrządem przeznaczonym do tego celu np. takim jak na poniższym rysunku. Głównym elementem tego przyrządu jest ruchomy tłok o powierzchni ΔS opierający się na sprężynie, mogący poruszać się w kierunku pionowym (a więc wzdłuż cylindra stanowiącego jednocześnie obudowę tego przyrządu).
Ciśnienie płynów – wzór
Odpowiednie wyskalowanie takiego czujnika pozwala odczytać długość o jaką sprężyna ulega przesunięciu wskutek oddziaływania płynu na powierzchnię tłoka. Długość ta jest jednocześnie miarą siły ΔF, z jaką płyn działa na tłok i podstawą do wyznaczenia wartości ciśnienia p (od angielskiego słowa pressure oznaczającego ciśnienie) wywieranego przez płyn, zdefiniowanego jako:
$$p = \frac{\Delta \hspace{.03cm} F}{\Delta \hspace{.03cm} S}$$
Dokładniej, ciśnienie w dowolnym punkcie płynu jest równe granicy tego ilorazu, gdy powierzchnia ΔS wokół tego punktu staje się coraz mniejsza i mniejsza (osiągając rozmiar tego punktu).
W przypadku, gdy wartość siły działającej na tłok będzie jednakowa w każdym punkcie powierzchni tłoka, tzn. w przypadku równomiernego nacisku na jego powierzchnię, powyższe równanie będzie można zapisać w następującej formie:
$$p = \frac{F}{S}$$
gdzie F to wartość siły działającej normalnie (prostopadle) na tłok o powierzchni S . Słowo „wartość siły” nie zostało przypadkowo wytłuszczone. Ciśnienie jest wielkością skalarną, a więc nie zależy od kierunku względem którego dokonujemy pomiaru (wartość siły jest właśnie skalarem).
Ciśnienie – jednostka
Jednostką ciśnienia w układzie SI jest N/m2, czyli paskal (ozn. Pa), nazwany tak na cześć francuskiego fizyka i matematyka Blaise Pascala (1623 – 1662). Innymi jednostkami ciśnienia, z którymi możesz się także spotkać jest atmosfera (ozn. atm), bar (ozn. bar), czy tor (ozn. Tr) nazywany również milimetrem słupa rtęci (ozn. mm Hg). Pomiędzy wymienionymi jednostkami ciśnienia a paskalem istnieje następująca zależność (podana dla średniej wartości ciśnienia atmosferycznego na poziomie morza):
$$1,\hspace{-.1cm}01 \cdot 10^5 \hspace{.05cm} \textrm{Pa} = 1,\hspace{-.1cm}01 \hspace{.05cm} \textrm{bar} = 1 \hspace{.05cm} \textrm{atm} = 760 \hspace{.05cm} \textrm{Tr}$$
W poniższej tabeli przedstawiono kilka wybranych wartości ciśnienia (na podstawie Tablice fizyczno – astronomiczne wyd. Adamantan):
| Ciśnienie (Pa) | |
|---|---|
| Przestrzeń międzygalaktyczna | 10-22 |
| Przestrzeń międzyplanetarna | 10-14 |
| Na szczycie Mount Everest (8848 m n.p.m.) | 3,3 ∙ 104 |
| Średnie ciśnienie atmosferyczne w Polsce | 1,01 ∙ 105 |
| Ciśnienie powietrza w oponie samochodowej | 2 ∙ 105 |
| W butelce szampana | 6 ∙ 105 |
| Pod obcasem buta (’szpilka’) | 2,5 ∙ 106 |
| Sprężanie paliwa w silniku Diesla | (3 – 9) ∙ 106 |
| W butli tlenowej dla nurków | 1,5 ∙ 107 |
| Dno Rowu Mariańskiego (10994 m p.p.m.) | 1,1 ∙ 108 |
| Igła w maszynie do szycia | 5 ∙ 108 |
| Jądro Ziemi | 3,7 ∙ 1011 |
| Wybuch bomby jądrowej | 5 ∙ 1013 |
| Wnętrze gwiazdy neutronowej | 1033 |

Dodaj komentarz