Wahadło torsyjne

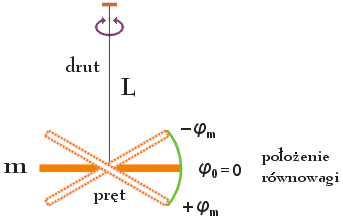
Wahadło torsyjne, nazywane również wahadłem skrętnym, to przykład oscylatora harmonicznego, w którym drgania układu związane są ze zmianą przemieszczenia kątowego φ (skręcenia) jednego z końców cienkiego drutu, którego drugi, nieruchomy koniec zamocowany jest w stałym punkcie. Na poniższym rysunku przedstawiono przykład takiego wahadła, w którym przemieszczeniu kątowemu φ  ulega pręt o masie m  zawieszony w środku na drucie o długości L.

Moment siły wahadła torsyjnego – odpowiednik siły sprężystości oscylatora harmonicznego

Obrót pręta o dowolny kąt φ  względem położenia równowagi pręta φ₀ = 0, powoduje powstanie drgań harmonicznych. Pręt zaczyna oscylować w płaszczyźnie poziomej wokół położenia równowagi, wykonując drgania z amplitudą zmian kąta wynoszącą φ_m . Podobnie jak zmiana wydłużenia sprężyny jest źródłem energii potencjalnej sprężystości sprężyny, tak i skręcenie drutu jest źródłem energii potencjalnej E_p  drutu. Energia ta powoduje powstanie momentu siły M dążącego do przywrócenia położenia równowagi pręta, o wartości:

$$M = \hspace{.1cm} – \hspace{.1cm} K \hspace{.05cm} \varphi$$

gdzie:
K  – stała proporcjonalności nazywana momentem kierującym (odpowiednik stałej sprężystości k sprężyny),
φ  – przemieszczenie kątowe pręta (odpowiednik przemieszczenia x  sprężyny).

Powyższe wyrażenie stanowi kątowy odpowiednik równania F = – k x, opisującego zależność siły F  od przemieszczenia x  sprężyny drgającej ruchem harmonicznym (zobacz: Siła w ruchu harmonicznym). W przypadku wahadła torsyjnego moment siły M  jest proporcjonalny do przemieszczenia kątowego φ  pręta.

Częstość kołowa i okres drgań wahadła torsyjnego – wzór

Ze względu na fakt, że moment siły M  jest liniowo proporcjonalny do przemieszczenia kątowego φ, wyrażenie na częstość kołową ω  oraz okres T  drgań wahadła torsyjnego uzyskamy korzystając ze wzorów na ω  i T  w liniowym ruchu harmonicznym:

$$\omega = \sqrt{\frac{\mathstrut k}{m}} \hspace{1cm} , \hspace{1cm} T = 2 \hspace{.05cm} \pi \sqrt{\frac{\mathstrut m}{k}}$$

Wstawiając w miejsce k  stałą K, zaś w miejsce m  wielkość I  będącą momentem bezwładności, w tym przypadku drgającego pręta, dostaniemy:

$$\omega = \sqrt{\frac{\mathstrut K}{I}}$$

oraz

$$T = 2 \hspace{.05cm} \pi \sqrt{\frac{\mathstrut I}{K}}$$