Wahadło matematyczne i fizyczne

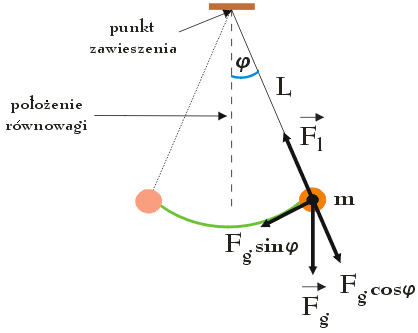
Wahadło matematyczne oraz wahadło fizyczne to przykłady oscylatora harmonicznego, którego drgania zachodzą w płaszczyźnie pionowej, pod wpływem siły grawitacji. Na początku zajmiemy się omówieniem wahadła matematycznego tj. wahadła mającego postać ciała o masie m  zawieszonego na jednym z końców nierozciągliwej linki o znikomej masie i o długości L, której drugi koniec zamocowany jest w stałym punkcie. Przykładem takiego wahadła jest układ ciężarek – linka przedstawiony na poniższym rysunku, wykonujący drgania w płaszczyźnie pionowej w kierunku z lewa na prawą.

Wahadło matematyczne – rozkład sił

Zgodnie z poniższym rysunkiem siłami działającymi na ciężarek są siła naprężenia linki F_l  oraz siła ciężkości F_g, skierowana równolegle do linii przerywanej oznaczającej położenie równowagi układu ciężarek – linka. Po rozłożeniu siły F_g  na składowe otrzymujemy składową radialną F_g cosφ, skierowaną przeciwnie do siły F_l  oraz składową F_g sinφ  – styczną do toru ruchu ciężarka. Podobnie jak w przypadku wahadła torsyjnego, także i w tym przypadku na ciężarek wykonujący drgania działa moment siły M, dążący do przywrócenia położenia równowagi ciężarka, o wartości:

$$M = \hspace{.15cm} – \hspace{.05cm} m \hspace{.05cm} g \hspace{.05cm} L \hspace{.05cm} \textrm{sin} \hspace{.05cm} \varphi$$

Za powstanie momentu siły M, działającego przeciwnie do wychylenia ciężarka (stąd znak minus w powyższym wyrażeniu), odpowiada składowa siły ciężkości F_g sinφ. W przybliżeniu małych kątów (φ  ≤ 5^o), tj. drgań o małej amplitudzie, częstość kołową ω  oraz okres T  drgań wahadła matematycznego możemy wyznaczyć korzystając z poniższych wzorów:

$$\omega = \sqrt{\frac{\mathstrut m \hspace{.05cm} g \hspace{.05cm} L}{I}}$$

oraz:

$$T = 2 \hspace{.05cm} \pi \hspace{.05cm} \sqrt{\frac{\mathstrut I}{m \hspace{.05cm} g \hspace{.05cm} L}}$$

gdzie:
m  – masa ciężarka,
g  – przyspieszenie ziemskie,
L  – odległość dzieląca punkt zawieszenia wahadła od środka jego masy,
I  – moment bezwładności wahadła względem jego punktu zawieszenia.

Częstość kołowa i okres drgań wahadła matematycznego – wzór

Zapisując moment bezwładności wahadła jako I  = mL², otrzymamy:

$$\omega = \sqrt{\frac{\mathstrut g}{L}}$$

oraz:

$$T = 2 \hspace{.05cm} \pi \hspace{.05cm} \sqrt{\frac{\mathstrut L}{g}}$$

Zasadniczą różnicą pomiędzy wahadłem matematycznym a wahadłem fizycznym jest rozkład ich masy. W przypadku wahadła matematycznego, jego całkowita masa skupiona jest w ciężarku zawieszonym na lince, znajdującym się w odległości L, odpowiadającej długości linki, od punktu jego zawieszenia. Rozkład masy wahadła fizycznego, nazywanego również wahadłem rzeczywistym, jest nieco bardziej skomplikowany w porównaniu z wahadłem matematycznym (patrz poniższy przykład).

Wahadło fizyczne – rozkład sił

Na poniższym rysunku przedstawiono przykładowe wahadło fizyczne, którego środek masy S  zlokalizowany jest w odległości h  od punktu zawieszenia wahadła.

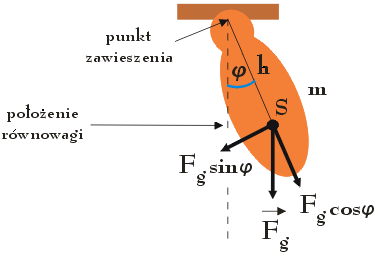
Podobnie jak w przypadku wahadła matematycznego, na wahadło fizyczne poruszające się ruchem okresowym, działa moment siły M  dążący do przywrócenia stanu równowagi tego wahadła. Jednakże w tym przypadku moment siły nie jest proporcjonalny do długości linki L, lecz do długości h  dzielącej punkt zawieszenia wahadła od punktu S  będącego środkiem masy wahadła:

$$M = \hspace{.15cm} – \hspace{.05cm} m \hspace{.05cm} g \hspace{.05cm} h \hspace{.05cm} \textrm{sin} \hspace{.05cm} \varphi$$

Częstość kołowa i okres drgań wahadła fizycznego – wzór

Wyrażenia pozwalające obliczyć częstość kołową ω  oraz okres T  drgań wahadła fizycznego wynoszą odpowiednio (dla małych kątów):

$$\omega = \sqrt{\frac{\mathstrut m \hspace{.05cm} g \hspace{.05cm} h}{I}}$$

oraz:

$$T = 2 \hspace{.05cm} \pi \hspace{.05cm} \sqrt{\frac{\mathstrut I}{m \hspace{.05cm} g \hspace{.05cm} h}}$$

Podstawiając w miejsce I /mh  wartość L₀  dostaniemy wzór na okres drgań wahadła matematycznego:

$$T = 2 \hspace{.05cm} \pi \hspace{.05cm} \sqrt{\frac{\mathstrut I}{m \hspace{.05cm} g \hspace{.05cm} h}} = 2 \hspace{.05cm} \pi \hspace{.05cm} \sqrt{\frac{\mathstrut L_0}{g}}$$

Z powyższej zależności wynika bardzo ważna informacja: każdemu wahadłu fizycznemu drgającemu z okresem T  wokół punktu zawieszenia, odpowiada wahadło matematyczne o długości L₀ (długość L₀  nazywana jest długością zredukowaną wahadła) drgające z takim samym okresem, co wahadło fizyczne.