Trzecie prawo Keplera – wyprowadzenie wzoru

Wyprowadzenie wzoru:

Zacznijmy od naszkicowania sytuacji, w której planeta o masie m  porusza się wokół Słońca (o masie M ) po orbicie kołowej o promieniu r. Promień r  orbity kołowej jest odpowiednikiem półosi wielkiej elipsy a  (zobacz: Prawa Keplera).

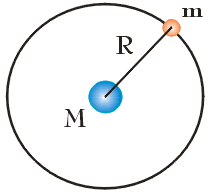
Ruch planety wokół Słońca odbywa się pod wpływem siły dośrodkowej, którą stanowi siła ich wzajemnego przyciągania grawitacyjnego:

$$F=G\frac{mM}{r^2}$$

Przyspieszenie dośrodkowe a  z jakim porusza się planeta wynosi:

$$a={\omega }^{2}r$$

gdzie ω to prędkość kątowa planety.

Zapisując dla tego układu drugą zasadę dynamiki Newtona, dostaniemy:

$${\overrightarrow{F}}_{wyp}=m\overrightarrow{a}⟶G\frac{mM}{r^2}=m{\omega }^{2}r$$

Po skróceniu oraz podzieleniu obydwu stron powyższego równania przez promień r, otrzymamy:

$$G\frac{M}{r^3}={\omega }^2$$

Prędkość kątową ω planety możemy wyrazić jako:

$$\omega =\frac{2\pi }{T}$$

gdzie T  to okres obiegu Słońca przez planetę.

Mamy więc:

$$G\frac{M}{r^3}={\left(\frac{2\pi }{T}\right)}^2$$

Po przekształceniu powyższego wyrażenia względem T, dostaniemy:

$$T^2=\frac{4{\pi }^2}{GM}{r}^3$$

Równanie, które otrzymaliśmy jest słuszne dla obiektów poruszających się po orbicie kołowej o promieniu r. Jak napisaliśmy wyżej, promień r  jest odpowiednikiem półosi wielkiej elipsy a, zatem dla ciał poruszających się po orbicie eliptycznej prawdziwe jest poniższe wyrażenie, które mieliśmy wyprowadzić:

$$T^2=\frac{4{\pi }^2}{GM}{a}^3$$