Prawo Pascala – zadanie nr 3

Do dwóch identycznych szklanych naczyń, w kształcie prostopadłościanów, które połączono rurką z zamkniętym zaworem Z (rysunek poniżej), nalano wody. Do jednego z nich wlano 1 litr wody, do drugiego 2 litry wody. Następnie zawór Z otwarto i po pewnym czasie w obydwu naczyniach ustalił się jednakowy poziom wody.

a) Oblicz stosunek ciśnień hydrostatycznych p₁ /p₂ wywieranych na dna naczyń 1 i 2 w sytuacjach przed otwarciem i po otwarciu zaworu, gdy ustali się stan równowagi.

b) Zapisz nazwę i treść prawa, do którego należy się odwołać, aby wyjaśnić, dlaczego poziomy cieczy w obu naczyniach po otwarciu zaworu wyrównały się.

Ciśnienie hydrostatyczne to ciśnienie wywierane przez płyn znajdujący się w stanie spoczynku. Wartość tego ciśnienia możemy obliczyć posługując się poniższym wzorem:

$$p = p_0 + \rho \hspace{.05cm} g \hspace{.05cm} h$$

Zarówno w sytuacji przed, jak i po otwarciu zaworu Z, najbardziej będzie nas interesować wysokość h  słupa wody w jednym oraz w drugim zbiorniku, ponieważ zgodnie z powyższym wzorem wartość ciśnienia hydrostatycznego jest ściśle związana z tą wysokością. Ciśnienie atmosferyczne p₀ działające na powierzchnię wody przyjmuje w obydwu zbiornikach jednakową wartość, w związku z czym będziemy je pomijać w dalszych obliczeniach.

Na początek skupmy się na pierwszym przypadku tj. w sytuacji przed otwarciem zaworu Z (zobacz: poniższy rysunek). Zawór Z jest zamknięty a więc przepływ cieczy pomiędzy naczyniami jest oczywiście niemożliwy.

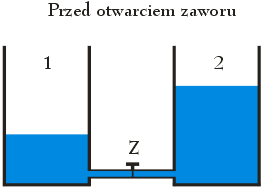
Wysokość słupów wody w obydwu zbiornikach nie jest znana, jednak możemy ją powiązać z objętością V  wody w zbiornikach, która jak wynika z treści zadania wynosi V₂ = 2 V₁. Ponieważ naczynia, w których znajduje się woda są identyczne, tak więc wysokość słupa wody w drugim naczyniu musi być dwukrotnie większa niż w naczyniu pierwszym: h₂ = 2 h₁. Po podstawieniu tych wartości do wzoru na ciśnienie dla jednego i drugiego zbiornika oraz następnie po podzieleniu ich przez siebie, otrzymamy:

$$\frac{p_1}{p_2} = \frac{ \rho \hspace{.05cm} g \hspace{.05cm} h_1}{ \rho \hspace{.05cm} g \hspace{.05cm} h_2} = \frac{h_1}{h_2} = \frac{h_1}{2 \hspace{.05cm} h_1} = \frac{1}{2}$$

Tak więc w sytuacji przed otwarciem zaworu Z stosunek ciśnień hydrostatycznych wywieranych na dno naczyń w jednym oraz w drugim zbiorniku wynosi 1/2.

Zajmijmy się teraz drugim przypadkiem. Jak się pewnie domyślasz, otwarcie zaworu Z spowoduje przepływ cieczy z naczynia drugiego do naczynia pierwszego, ponieważ wysokość słupa wody w drugim naczyniu jest większa od wysokości słupa w naczyniu pierwszym. Przepływ wody będzie zachodził tak długo, dopóki jej poziom w obydwu zbiornikach nie będzie jednakowy (zobacz poniższy rysunek).

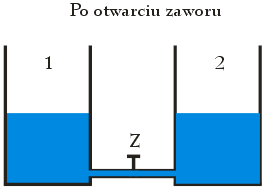
W momencie, w którym wysokość słupa wody w jednym oraz w drugim naczyniu będzie jednakowa, wartość ciśnienia hydrostatycznego wywieranego przez wodę na dno tych zbiorników będzie przyjmować w obydwu przypadkach taką samą wartość. Oznacza to, że stosunek ciśnień będzie równy:

$$\frac{p_1}{p_2} = \frac{\rho \hspace{.05cm} g \hspace{.05cm} h}{\rho \hspace{.05cm} g \hspace{.05cm} h} = 1$$

Proces przepływu cieczy pomiędzy naczyniami związany jest z wytworzeniem się różnicy ciśnień Δp, która zgodnie z prawem Pascala przenoszona jest bez zmiany wartości do każdego miejsca w płynie oraz do ścian zbiornika.