Zwierciadło płaskie, wklęsłe i wypukłe – zadanie nr 6

Promień krzywizny zwierciadła sferycznego wklęsłego jest równy r  = 0,5 m. Znajdź odległość obrazu od środka zwierciadła, jeżeli przedmiot znajduje się w jego ognisku.

Aby wyznaczyć odległość obrazu od środka zwierciadła wklęsłego skorzystamy z równania zwierciadła sferycznego:

$$\frac{1}{x} + \frac{1}{y} = \frac{1}{f}$$

gdzie:
x  – odległość przedmiotu od środka zwierciadła,
y  – odległość obrazu od środka zwierciadła,
f  – ogniskowa zwierciadła.

Zarówno wartość x,  jak i f  nie jest podana w treści zadania. Wiemy jednak, że przedmiot znajduje się w ognisku zwierciadła oraz, że promień krzywizny zwierciadła wynosi r  = 0,5 m. Odległość dzieląca środek zwierciadła od jego ogniska odpowiada ogniskowej f  zwierciadła, w związku z czym x  = f. Po wstawieniu tej zależności do równania zwierciadła sferycznego dostaniemy:

$$\frac{1}{f} + \frac{1}{y} = \frac{1}{f}$$

i w konsekwencji:

$$\frac{1}{y} = \frac{1}{f} \hspace{.1cm} – \hspace{.1cm} \frac{1}{f} = 0$$

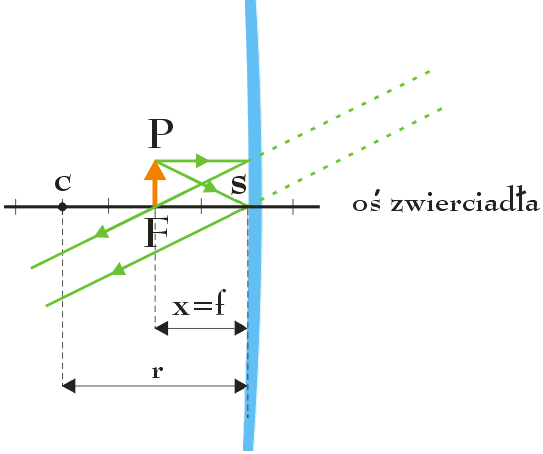
Aby powyższa równość była spełniona obraz przedmiotu musi znajdować się w nieskończoności (y  = +∞ lub y  = -∞). Oznacza to, że obraz przedmiotu umieszczonego w ognisku zwierciadła sferycznego wklęsłego nigdy nie powstanie, ponieważ ani promienie odbite, ani przedłużenia tych promieni nie będą się przecinały. Potwierdzeniem tej sytuacji jest poniższy rysunek: