Zwierciadło płaskie, wklęsłe i wypukłe – zadanie nr 5
W którym punkcie głównym osi optycznej zwierciadła sferycznego wklęsłego o ogniskowej f = 10 cm należy umieścić przedmiot, aby otrzymać obraz prosty, pozorny, dwukrotnie powiększony? Wynik obliczeń sprawdź na rysunku.
Wielkością szukaną w zadaniu jest odległość x dzieląca przedmiot od środka zwierciadła, dla której obraz przedmiotu jest obrazem pozornym, prostym oraz podwójnie powiększonym. Zgodnie z teorią obraz pozorny dowolnego przedmiotu, wytwarzany przez zwierciadło sferyczne wklęsłe, możemy otrzymać tylko wtedy, gdy x < f . Takiego właśnie wyniku spodziewamy się w tym zadaniu.
Aby wyznaczyć odległość x przedmiotu skorzystamy z równania zwierciadła sferycznego:
$$\frac{1}{x} + \frac{1}{y} = \frac{1}{f}$$
gdzie:
y – odległość dzieląca obraz przedmiotu od środka zwierciadła,
f – ogniskowa zwierciadła.
Wartość ogniskowej f znamy. Odległość y powiążemy z powiększeniem liniowym p zwierciadła. Wiemy, że obraz przedmiotu jest dwukrotnie powiększony, dlatego:
$$p = \hspace{.1cm} – \hspace{.1cm} \frac{y}{x} = 2$$
Obraz przedmiotu jest obrazem prostym (ma taką samą orientację co przedmiot), dlatego też powiększenie liniowe p zwierciadła przyjmuje wartość dodatnią.
Po przekształceniu powyższego wzoru względem odległości y, dostaniemy:
$$\hspace{.1cm} – \hspace{.1cm} \frac{y}{x} = 2 \hspace{1cm} \longrightarrow \hspace{1cm} y = \hspace{.1cm} – \hspace{.1cm} 2 \hspace{.05cm} x$$
Wstawiając otrzymane wyrażenie do równania zwierciadła sferycznego uzyskamy:
$$\frac{1}{x} + \frac{1}{y} = \frac{1}{f} \hspace{1cm} \longrightarrow \hspace{1cm} \frac{1}{x} \hspace{.1cm} – \hspace{.1cm} \frac{1}{2 \hspace{.05cm} x} = \frac{1}{2 \hspace{.05cm} x} = \frac{1}{f}$$
i w konsekwencji szukaną wartość x równą:
$$\frac{1}{2 \hspace{.05cm} x} = \frac{1}{f} \hspace{1cm} \longrightarrow \hspace{1cm} x = \tfrac{1}{2} \hspace{.05cm} f = \tfrac{1}{2} \cdot 10 \hspace{.05cm} \textrm{cm} = 5 \hspace{.05cm} \textrm{cm}$$
Zwróć uwagę, że zgodnie z oczekiwaniami, odległość x jest mniejsza od ogniskowej f zwierciadła, świadcząc tym samym o poprawności otrzymanego wyniku. Dodatkowe potwierdzenie stanowi poniższy rysunek:
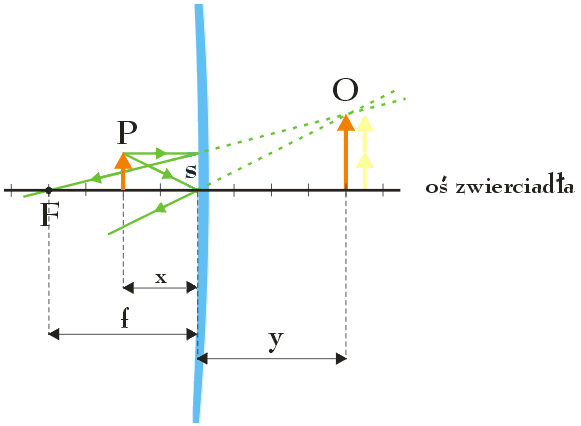

Dodaj komentarz