Zwierciadło płaskie, wklęsłe i wypukłe – zadanie nr 4
Przed zwierciadłem sferycznym wklęsłym o promieniu krzywizny r = 30 cm umieszczono w odległości x = 20 cm płonącą świecę o wysokości h = 10 cm. W jakiej odległości od zwierciadła i jakiej wysokości powstanie obraz? Określ cechy tego obrazu.
Zadanie to rozwiążemy dwoma (równoważnymi sobie) sposobami. Na początku wyznaczymy odległość i wysokość obrazu korzystając z metody konstrukcyjnej, by później porównać otrzymane wartości z wynikami uzyskanymi dzięki zastosowaniu metody obliczeniowej. Ponieważ położenie, rodzaj oraz orientacja obrazu przedmiotu wytwarzanego przez zwierciadło sferyczne wklęsłe zależy od położenia tego przedmiotu względem środka zwierciadła wklęsłego, dlatego przed sporządzeniem odpowiedniego rysunku musimy wyznaczyć długość ogniskowej tego zwierciadła. Ogniskowa f zwierciadła sferycznego powiązana jest z jego promieniem krzywizny r poniższą zależnością:
$$f = \tfrac{1}{2} \hspace{.05cm} r$$
Wiedząc, że r = 0,3 m dostaniemy:
$$f = \tfrac{1}{2} \hspace{.05cm} r = \tfrac{1}{2} \cdot 0,\hspace{-.1cm}3 \hspace{.05cm} \textrm{m} = 0,\hspace{-.1cm}15 \hspace{.05cm} \textrm{m}$$
Znając odległość przedmiotu od środka zwierciadła równą x = 0,2 m oraz długość ogniskowej f = 0,15 m możemy przystąpić do konstrukcyjnego wyznaczenia obrazu przedmiotu. Ponieważ x jest nieznacznie większe od f, dlatego spodziewamy się, że obraz świecy będzie obrazem rzeczywistym, odwróconym oraz powiększonym.
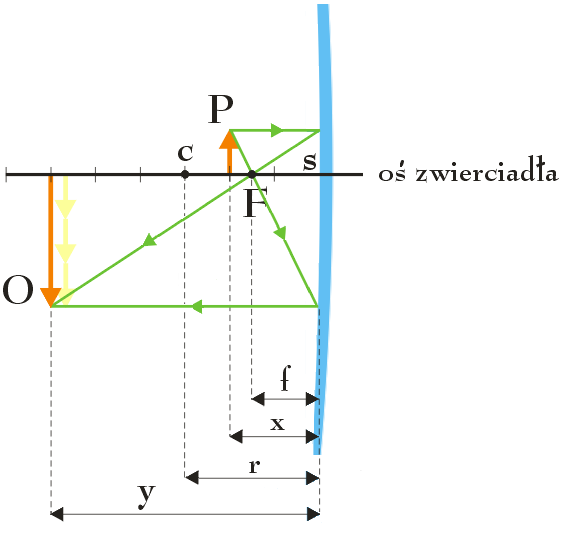
Zgodnie z powyższym rysunkiem (oraz naszymi oczekiwaniami) obraz płonącej świecy jest obrazem rzeczywistym, odwróconym oraz trzykrotnie powiększonym, w związku z czym wysokość h’ obrazu O wynosi h’ = 3 ∙ h = 30 cm. Odległość obrazu O od środka s zwierciadła wynosi z kolei y = 60 cm (szczegóły w opisie rysunku).
Aby sprawdzić poprawność wykonanej konstrukcji obrazu, przeprowadzimy obliczenia. Odległość obrazu y wyznaczymy z równania zwierciadła sferycznego:
$$\frac{1}{x} + \frac{1}{y} = \frac{1}{f}$$
które po przekształceniu względem y przyjmie poniższą postać:
$$\frac{1}{y} = \frac{1}{f} \hspace{.1cm} – \hspace{.1cm} \frac{1}{x} = \frac{x \hspace{.1cm} – \hspace{.1cm} f}{x \cdot f} \hspace{1cm} \longrightarrow \hspace{1cm} y = \frac{x \cdot f}{x \hspace{.1cm} – \hspace{.1cm} f}$$
Po wstawieniu wartości liczbowych x i f oraz po wykonaniu obliczeń otrzymamy:
$$y = \frac{0,\hspace{-.1cm}2 \hspace{.05cm} \textrm{m} \cdot 0,\hspace{-.1cm}15 \hspace{.05cm} \textrm{m}}{0,\hspace{-.1cm}2 \hspace{.05cm} \textrm{m} \hspace{.1cm} – \hspace{.1cm} 0,\hspace{-.1cm}15 \hspace{.05cm} \textrm{m}} = 0,\hspace{-.1cm}6 \hspace{.05cm} \textrm{m}$$
Zwróć uwagę, że wynik ten jest zgodny z wartością y odczytaną z rysunku.
Następnie korzystając z poniższego wzoru opisującego powiększenie liniowe p zwierciadła sferycznego, obliczymy wysokość obrazu:
$$p = \hspace{.1cm} – \hspace{.1cm} \frac{y}{x}$$
Wartości x oraz y są znane, dlatego:
$$p = \hspace{.1cm} – \hspace{.1cm} \frac{0,\hspace{-.1cm}6 \hspace{.05cm} \textrm{m}}{0,\hspace{-.1cm}2 \hspace{.05cm} \textrm{m}} = \hspace{.1cm} – \hspace{.1cm} 3$$
Znak minus, stojący przed wartością liczbową, informuje nas, że obraz przedmiotu jest obrazem odwróconym (zobacz rysunek), z kolei wartość liczbowa mówi nam, że obraz przedmiotu jest trzykrotnie powiększony. W związku z powyższym możemy stwierdzić, że wysokość h’ obrazu wynosi h’ = 3 ∙ h = 30 cm, co oznacza, że wynik otrzymany przy zastosowaniu metody konstrukcyjnej jest wynikiem prawidłowym.

Dodaj komentarz