Szeregowe i równoległe łączenie kondensatorów
Układ kondensatorów połączonych szeregowo albo równolegle można znacznie uprościć poprzez zastąpienie go jednym, równoważnym kondensatorem o pojemności zastępczej CZ . W tym artykule zajmiemy się opisem i wyprowadzeniem wzorów pozwalających obliczyć pojemność zastępczą kondensatorów połączonych w sposób szeregowy oraz równoległy.
Szeregowe połączenie kondensatorów
Rysunek 1 przedstawia prosty obwód elektryczny składający się ze źródła prądu oraz z trzech kondensatorów o pojemnościach C1, C2 i C3 połączonych szeregowo. Zadaniem źródła jest utrzymywanie stałej różnicy potencjałów U w obwodzie.

W szeregowym sposobie łączenia kondensatorów wszystkie kondensatory łączone są ze sobą w szereg, jeden za drugim: ujemnie naładowana okładka kondensatora C1 łączy się z dodatnio naładowaną okładką kondensatora C2, z kolei ujemnie naładowana okładka kondensatora C2 łączy się z dodatnio naładowaną okładką kondensatora C3. Zwróć uwagę, że zgodnie z powyższym rysunkiem różnica potencjałów U przyłożona jest tylko do obydwu końców układu kondensatorów: biegun dodatni źródła połączony jest z dodatnio naładowaną okładką kondensatora C1, a biegun ujemny – z ujemnie naładowaną okładką kondensatora C3.
Źródło prądu podłączone do kondensatorów połączonych szeregowo wytwarza ładunki tylko i wyłącznie na tych okładkach kondensatorów, które są bezpośrednio połączone z biegunami źródła. Ładunki elektryczne na pozostałych okładkach pojawiają się wskutek przemieszczania się ładunków już istniejących (przemieszczaniu ulegają ładunki zgromadzone na okładkach kondensatorów połączonych z biegunami źródła). Zgodnie z rysunkiem 1 źródło prądu nie może zmienić ładunku na kondensatorze C2 (brak bezpośredniego połączenia ze źródłem) – ładunek na okładkach tego kondensatora pojawia się jako efekt przesuwania się ładunku z okładek kondensatora C3.
Aby uprościć układ kondensatorów przedstawionych na rysunku 1 możemy zastąpić je równoważnym im kondensatorem o pojemności CZ . Kondensator CZ posiada jednakowy ładunek oraz jednakową różnicę potencjałów, jak układ szeregowo połączonych kondensatorów.
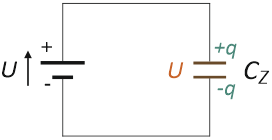
Nadszedł więc czas, aby wyprowadzić ogólne wyrażenie pozwalające obliczać pojemność zastępczą układu kondensatorów połączonych w sposób szeregowy. Na początek zapiszmy wyrażenia opisujące różnicę potencjałów na każdym z trzech kondensatorów z rysunku 1. Korzystając ze wzoru q = C U (zobacz: Kondensatory – opis, budowa. Pojemność elektryczna) i przekształcając je względem U, mamy:
$$U_1 = \dfrac{q}{C_1} \hspace{1cm} , \hspace{1cm} U_2 = \dfrac{q}{C_2} \hspace{1cm} , \hspace{1cm} U_3 = \dfrac{q}{C_3}$$
(zgodnie z tym co napisaliśmy wyżej, ładunek zgromadzony na każdym kondensatorze przyjmuje jednakową wartość)
Wiemy, że całkowita różnica potencjałów wytwarzana przez źródło jest sumą różnic potencjałów na wszystkich kondensatorach połączonych szeregowo, dlatego:
$$U = U_1 + U_2 + U_3 = \dfrac{q}{C_1} + \dfrac{q}{C_2} + \dfrac{q}{C_3} = q \left( \dfrac{1}{C_1} + \dfrac{1}{C_2} + \dfrac{1}{C_3} \right)$$
Różnica potencjałów na kondensatorze CZ wynosi:
$$U = \dfrac{q}{C_Z}$$
Porównując stronami wyrażenia na U, mamy:
$$\dfrac{q}{C_Z} = q \left( \dfrac{1}{C_1} + \dfrac{1}{C_2} + \dfrac{1}{C_3} \right)$$
Pojemność zastępcza kondensatorów połączonych szeregowo – wzór
Po skróceniu stronami powyższej zależności, dostaniemy:
$$\dfrac{1}{C_Z} = \dfrac{1}{C_1} + \dfrac{1}{C_2} + \dfrac{1}{C_3}$$
W ogólności, w przypadku n kondensatorów połączonych szeregowo pojemność zastępczą CZ możemy obliczyć stosując poniższe wyrażenie:
$$\dfrac{1}{C_Z} = \sum\limits_{i=1}^n \dfrac{1}{C_i} = \dfrac{1}{C_1} + \dfrac{1}{C_2} + … + \dfrac{1}{C_n}$$
gdzie Ci to pojemność i-tego kondensatora w obwodzie.
Równoległe połączenie kondensatorów
Podobnie jak w przypadku szeregowego układu kondensatorów, zacznijmy od narysowania obwodu elektrycznego składającego się ze źródła prądu oraz układu kondensatorów o pojemnościach C1, C2 i C3 , tym razem, połączonych równolegle:
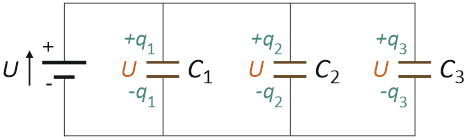
Równoległy sposób łączenia kondensatorów to taki, w którym zarówno jedne, jak i drugie okładki kondensatorów łączone są bezpośrednio ze sobą za pomocą wspólnych przewodów. Ponieważ, różnica potencjałów U przykładana jest właśnie do tych dwóch (połączonych przewodami) okładek, dlatego też:
Kondensatory połączone równolegle możemy zastąpić równoważnym im kondensatorem o pojemności zastępczej CZ . Kondensator CZ posiada jednakowy ładunek oraz jednakową różnicę potencjałów, jak układ równolegle połączonych kondensatorów.
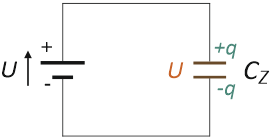
Aby wyprowadzić ogólne wyrażenie pozwalające obliczyć pojemność zastępczą kondensatora CZ , równoważnego kondensatorom połączonym równolegle, zacznijmy od zapisania zależności opisujących ładunek elektryczny zgromadzony na każdym z trzech kondensatorów z rysunku 3:
$$q_1 = C_1 \hspace{.05cm} U \hspace{1cm} , \hspace{1cm} q_2 = C_2 \hspace{.05cm} U \hspace{1cm} , \hspace{1cm} q_3 = C_3 \hspace{.05cm} U$$
Całkowity ładunek zgromadzony w układzie tych trzech kondensatorów wynosi więc:
$$q = q_1 + q_2 + q_3 = C_1 \hspace{.05cm} U + C_2 \hspace{.05cm} U + C_3 \hspace{.05cm} U = U \left( C_1 + C_2 + C_3 \right)$$
Wiemy, że całkowity ładunek elektryczny zgromadzony na kondensatorze CZ z rysunku 4 również jest równy q, w związku z czym:
$$q = C_Z \hspace{.05cm} U$$
Po przyrównaniu stronami wzorów na ładunek q, otrzymamy:
$$C_Z \hspace{.05cm} U = U \left( C_1 + C_2 + C_3 \right)$$
Pojemność zastępcza kondensatorów połączonych równolegle – wzór
Po skróceniu stronami powyższej zależności, dostaniemy:
$$C_Z = C_1 + C_2 + C_3$$
W ogólności, w przypadku n kondensatorów połączonych równolegle pojemność zastępczą CZ możemy obliczyć stosując poniższe wyrażenie:
$$C_Z = \sum\limits^n_{i = 1} C_i = C_1 + C_2 + … + C_n$$

2 komentarze
Paula
Dodano dnia 7 września 2021 o godz. 21:27
Bardzo przydana treść!
Leon
Dodano dnia 1 marca 2021 o godz. 09:00
Fizyka zawsze mnie rajcowała i tak mi zostało.