Pojemność kondensatora płaskiego, walcowego i kulistego
Pojemność elektryczna kondensatora to wielkość fizyczna będąca miarą ilości ładunku elektrycznego q, jaki należy umieścić na okładkach kondensatora, aby wytworzyć między nimi różnicę potencjałów U. W artykule Kondensatory – opis, budowa. Pojemność elektryczna napisaliśmy, że pojemność kondensatora zależy tylko i wyłącznie od jego geometrii, jednak nie poparliśmy tego żadnymi wzorami. W tym artykule zajmiemy się opisem oraz podamy wyrażenia na pojemność elektryczną kondensatora płaskiego, walcowego oraz kulistego.
Pojemność elektryczna kondensatora płaskiego
Kondensator płaski składa się z dwóch równoległych, przewodzących prąd elektryczny okładek o polu powierzchni S , znajdujących się od siebie w odległości równej d. Na poniższym rysunku przedstawiono przekrój kondensatora płaskiego z zaznaczeniem ładunku zgromadzonego na powierzchni jego okładek oraz pola elektrycznego $\vec{E}$ występującego między tymi okładkami:
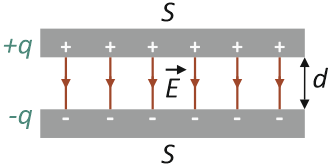
Kondensator płaski bez materiału izolującego
Gdy obszar pomiędzy okładkami kondensatora płaskiego wypełnia próżnia, wówczas wzór pozwalający obliczyć pojemność elektryczną tego kondensatora przedstawia się następująco:
$$C = \varepsilon_0 \hspace{.05cm} \dfrac{S}{d}$$
gdzie ε0 to przenikalność elektryczna próżni (ε0 = 8,85 ⋅ 10-12 F/m – możemy też wyrazić tą wielkość w jednostce C2/(N ⋅ m2)), S – powierzchnia pojedynczej okładki kondensatora, a d to odległość pomiędzy okładkami kondensatora.
Powyższa zależność potwierdza to, co napisaliśmy w artykule Kondensatory – opis, budowa. Pojemność elektryczna: pojemność elektryczna kondensatora zależy tylko i wyłącznie od jego geometrii (wielkość S i d ). Zwróć uwagę, że im większe pole powierzchni okładek oraz im mniejsza odległość pomiędzy okładkami, tym większa pojemność elektryczna kondensatora płaskiego.
Kondensator płaski z materiałem izolującym
Wzór na pojemność kondensatora płaskiego ulegnie nieznacznej zmianie, gdy przestrzeń między jego okładkami będzie wypełniona materiałem izolującym (dielektrykiem). Okazuje się, że w takim przypadku wzór na pojemność C kondensatora płaskiego będzie równy:
$$C = \varepsilon_0 \hspace{.1cm} \varepsilon_r \hspace{.05cm} \dfrac{S}{d}$$
gdzie εr to względna przenikalność elektryczna materiału izolującego (wielkość ta jest bezwymiarowa tj. nie posiada jednostki).
W oparciu o powyższą zależność możemy stwierdzić, że umieszczenie dielektryka między okładkami kondensatora powoduje wzrost jego pojemności o wielkość εr. W poniższej tabeli podano wartość εr dla wybranych izolatorów:
| Materiał izolujący | Względna przenikalność elektryczna εr (-) |
|---|---|
| Próżnia | 1 |
| Powietrze | 1,00054 |
| Polistyren | 2,4 |
| Papier | 3,5 |
| Porcelana | 6,5 |
| Guma | 7 |
| Grafit | 10 |
| Krzem | 12 |
| German | 16 |
| Woda (temp. 20 oC) | 80 |
| Woda (temp. 0 oC) | 88 |
| Lód | 100 |
Materiały izolacyjne oprócz względnej przenikalności elektrycznej charakteryzują się m.in. tzw. wytrzymałością na przebicie. Parametr ten opisuje maksymalną wartość natężenia pola elektrycznego, jaką dielektryk może wytrzymać bez przebicia. Aby izolator nie uległ uszkodzeniu (przebiciu), napięcie między okładkami kondensatora musi być mniejsze od napięcia przebicia. Gdy napięcie przebicia zostanie przekroczone dielektryk ulegnie uszkodzeniu, a konsekwencją tego zjawiska będzie powstanie przewodzącej ścieżki między okładkami kondensatora.
Pojemność elektryczna kondensatora walcowego
Kondensator walcowy składa się z dwóch współosiowych powierzchni walcowych o promieniach r1 oraz r2 i długości l, przy czym l ≫ r1 oraz l ≫ r2. Poniższy rysunek przedstawia przekrój kondensatora walcowego z zaznaczeniem obydwu powierzchni walcowych oraz zgromadzonego na nich ładunku elektrycznego:
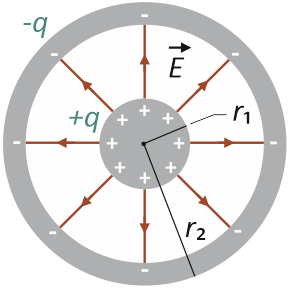
Pojemność elektryczną kondensatora walcowego możemy obliczyć stosując poniższe wzory:
– bez materiału izolującego między okładkami:
$$C = 2 \hspace{.05cm} \pi \hspace{.05cm} \varepsilon_0 \hspace{.1cm} \dfrac{l}{\textrm{ln} \hspace{.05cm} r_2 \hspace{.15cm} – \hspace{.1cm} \textrm{ln} \hspace{.05cm} r_1}$$
– z materiałem izolującym między okładkami:
$$C = 2 \hspace{.05cm} \pi \hspace{.05cm} \varepsilon_0 \hspace{.05cm} \varepsilon_r \hspace{.1cm} \dfrac{l}{\textrm{ln} \hspace{.05cm} r_2 \hspace{.15cm} – \hspace{.1cm} \textrm{ln} \hspace{.05cm} r_1}$$
gdzie l to długość okładki kondensatora walcowego, a r1 i r2 to odpowiednio promień wewnętrznej oraz zewnętrznej okładki (w tym przypadku pod pojęciem ‘okładki’ rozumiemy obydwie powierzchnie walcowe kondensatora walcowego).
Pojemność elektryczna kondensatora kulistego
Kondensator kulisty składa się z dwóch współśrodkowych powłok sferycznych o promieniach r1 i r2. Przekrój przez środek kondensatora kulistego wygląda identycznie jak przekrój kondensatora walcowego przedstawionego na powyższym rysunku. Aby obliczyć pojemność elektryczną tego kondensatora należy skorzystać z poniższych wyrażeń:
– bez materiału izolującego między okładkami:
$$C = 4 \hspace{.05cm} \pi \hspace{.05cm} \varepsilon_0 \hspace{.1cm} \dfrac{r_1 \hspace{.05cm} r_2}{r_2 \hspace{.15cm} – \hspace{.1cm} r_1}$$
– z materiałem izolującym między okładkami:
$$C = 4 \hspace{.05cm} \pi \hspace{.05cm} \varepsilon_0 \hspace{.05cm} \varepsilon_r \hspace{.1cm} \dfrac{r_1 \hspace{.05cm} r_2}{r_2 \hspace{.15cm} – \hspace{.1cm} r_1}$$
gdzie r1 i r2 to odpowiednio promień wewnętrznej oraz zewnętrznej okładki (w tym przypadku pod pojęciem ‘okładki’ rozumiemy obydwie powłoki sferyczne kondensatora kulistego).

Dodaj komentarz