Natężenie pola elektrycznego – zadanie nr 1

Dwa równe i różnoimienne ładunki o wielkości 2 ⋅ 10^-7 C znajdują się w odległości 15 cm od siebie.

a) Jaka jest wielkość i kierunek natężenia pola elektrycznego w środku odległości pomiędzy ładunkami?

b) Jaka siła (wielkość i kierunek) działałaby na elektron umieszczony w tym punkcie?

Przypadek a)

Zgodnie z definicją wartość natężenia pola elektrycznego $\overrightarrow{E}$  wytwarzanego przez naładowaną cząstkę, nazywaną również ‘ładunkiem punktowym’, możemy obliczyć posługując się poniższym wzorem:

$$E=\frac{1}{4\pi {\epsilon }_0}\frac{q}{r^2}=k\frac{q}{r^2}$$

gdzie:
k  – stała elektrostatyczna równa 9 ⋅ 10⁹ N ⋅ m²/C²,
q  – ładunek naładowanej cząstki,
r  – odległość pomiędzy środkiem cząstki, a punktem, w którym chcemy obliczyć natężenie pola elektrycznego.

Zgodnie z teorią linie sił pola elektrycznego dla ciała naładowanego dodatnio skierowane są od tego ciała (na zewnątrz), a dla ciała naładowanego ujemnie – skierowane do tego ciała (do wewnątrz). W pierwszej części zadania mamy obliczyć wartość oraz kierunek natężenia pola elektrycznego w środku odległości pomiędzy dwoma jednakowo naładowanymi różnoimiennymi ładunkami – ładunki różnoimienne to ładunki o przeciwnych znakach. Na potrzeby zadania jeden z tych ładunków oznaczymy jako q₁, drugi z nich jako q₂. Załóżmy ponadto, że ładunek q₁ jest naładowany dodatnio – q₁ = + 2 ⋅ 10^-7 C, a ładunek q₂ jest naładowany ujemnie – q₂ = – 2 ⋅ 10^-7 C. Ponieważ pierwszy ładunek jest naładowany dodatnio zatem wektor natężenia pola elektrycznego dla tego ładunku będzie zwrócony na zewnątrz (tj. od niego), z kolei wektor natężenia pola dla ładunku drugiego będzie zwrócony w stronę tego ładunku, czyli tak jak pokazano to na poniższym rysunku:

Zauważ, że wektory natężenia pola elektrycznego dla pierwszego oraz drugiego ładunku zwrócone są w tą samą stronę, zatem zwrot wypadkowego wektora natężenia pola elektrycznego musi być zgodny ze zwrotem tych dwóch wektorów (tj. zwrócony w stronę ładunku q₂). Aby obliczyć wypadkową wartość natężenia pola elektrycznego skorzystamy z poniższego wzoru (wektory ${\overrightarrow{E}}_1$  i  ${\overrightarrow{E}}_2$ mają ten sam zwrot, zatem wypadkowa wartość natężenia pola jest równa sumie wartości pola tych dwóch ładunków):

$$E_{wyp}=E_1+E_2=k\frac{|q_1|}{{\left(\frac{r}{2}\right)}^2}+k\frac{|q_2|}{{\left(\frac{r}{2}\right)}^2}=\frac{4k}{r^2}(|q_1|+|q_2|)$$

gdzie r  to odległość pomiędzy ładunkami.

Po podstawieniu do powyższego wzoru wartości liczbowych oraz wykonaniu obliczeń, dostaniemy wartość natężenia pola elektrycznego w połowie odległości pomiędzy ładunkami, równą:

$$E_{wyp}=\frac{4\cdot 9\cdot {10}^9\frac{\text{N}\cdot {\text{m}}^2}{{\text{C}}^2}}{{(0,15\text{m})}^2}\cdot (|2\cdot {10}^{-7}\text{C}|+|–2\cdot {10}^{-7}\text{C}|)=640000\frac{\text{N}}{\text{C}}$$

Przypadek b)

Zajmijmy się teraz drugą częścią zadania. Tym razem mamy obliczyć siłę wypadkową z jaką na elektron, umieszczony w połowie odległości pomiędzy ładunkami, działałyby te dwa ładunki. Sytuację tą przedstawia poniższy rysunek:

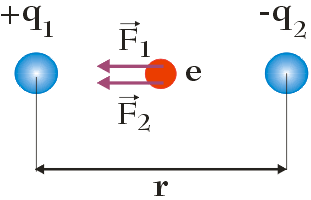
Elektron to cząstka naładowana ujemnie w związku z czym oddziaływanie elektrostatyczne pomiędzy elektronem, a ładunkiem q₁ (naładowanym dodatnio) będzie miało charakter przyciągający, z kolei pomiędzy elektronem, a ładunkiem q₂ (naładowanym ujemnie) – charakter odpychający. Ponieważ siły te mają ten sam zwrot, zatem siła wypadkowa działająca na elektron będzie posiadać zwrot zgodny ze zwrotem tychże sił (tj. w kierunku ładunku q₁). Aby obliczyć wartość siły wypadkowej działającej na elektron skorzystamy z prawa Coulomba opisującego siłę oddziaływania elektrostatycznego pomiędzy ładunkami:

$$F=\frac{1}{4\pi {ϵ}_0}\frac{|q_1||q_2|}{r^2}=k\frac{|q_1||q_2|}{r^2}$$

Wyrażenie na siłę wypadkową działającą na elektron będzie więc równe:

$$F_{wyp}=F_1+F_2=k\frac{|q_1||e|}{{\left(\frac{r}{2}\right)}^2}+k\frac{|q_2||e|}{{\left(\frac{r}{2}\right)}^2}=\frac{4k|e|}{r^2}(|q_1|+|q_2|)$$

gdzie e  to ładunek elektronu równy 1,6021 ⋅ 10^-19 C.

Po podstawieniu do powyższego wyrażenia wartości liczbowych oraz wykonaniu obliczeń, otrzymamy F_wyp , równe:

$$F_{wyp}=\frac{4\cdot 9\cdot {10}^9\frac{\text{N}\cdot {\text{m}}^2}{{\text{C}}^2}\cdot 1,6021\cdot {10}^{-19}\text{C}}{{(0,15\text{m})}^2}\cdot (|2\cdot {10}^{-7}\text{C}|+|–2\cdot {10}^{-7}\text{C}|)=1\cdot {10}^{-13}\text{N}$$