Prawo Coulomba

Prawo Coulomba to podstawowe prawo elektrostatyki, czyli działu fizyki zajmującego się zjawiskami związanymi z oddziaływaniami występującymi pomiędzy nieruchomymi (statycznymi) obiektami obdarzonymi ładunkiem elektrycznym. Na poniższym rysunku przedstawiono dwa ładunki punktowe naładowane albo dodatnio albo ujemnie, z zaznaczeniem sił (brązowe strzałki), jakimi te dwa ładunki oddziałują na siebie wzajemnie.

Oddziaływania elektrostatyczne pomiędzy ładunkami

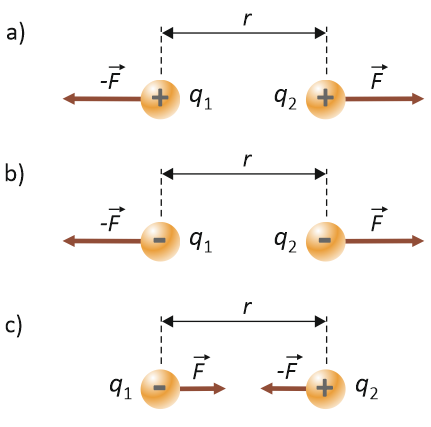
W pierwszym oraz w drugim przypadku mamy do czynienia z dwoma ładunkami punktowymi naładowanymi, odpowiednio, dodatnio oraz ujemnie. Jeżeli obydwa ciała naładowane są ładunkiem tego samego znaku (mówimy: naładowane jednoimiennie, tzn. dodatnio lub ujemnie), wówczas oddziaływanie elektrostatyczne pomiędzy ładunkami ma charakter odpychający (np. pomiędzy dwoma protonami lub dwoma elektronami) – strzałki, oznaczające siły, są skierowane na zewnątrz od każdego ładunku. W przeciwnym wypadku, tzn. gdy dwa ciała naładowane są ładunkiem o przeciwnych znakach (mówimy: naładowane różnoimiennie), czyli tak jak w trzeciej sytuacji na powyższym rysunku, oddziaływanie elektrostatyczne ma charakter przyciągający (np. pomiędzy elektronem a protonem w atomie wodoru) – strzałki skierowane są do wewnątrz każdego z tych ładunków.

Prawo Coulomba – wzór

Prawo Coulomba zostało sformułowane w 1785 roku przez francuskiego fizyka Charlesa Augustina Coulomba (1736-1806). Prawo to opisuje wielkość siły elektrostatycznego oddziaływania pomiędzy dwoma naładowanymi elektrycznie obiektami (np. elektronami, protonami) oddalonymi od siebie o wielkość r  (r  to odległość pomiędzy środkami ładunków, jak pokazano to na powyższym rysunku):

$$F = \frac{1}{4 \hspace{.05cm} \pi \hspace{.05cm} \epsilon_0} \frac{|q_1| \hspace{.05cm} |q_2|}{r^2} = k \hspace{.05cm} \frac{|q_1| \hspace{.05cm} |q_2|}{r^2}$$

gdzie:
q₁  – ładunek elektryczny pierwszego obiektu,
q₂  – ładunek elektryczny drugiego obiektu,
ε₀  – przenikalność elektryczna próżni równa 8,85 ∙ 10^-12 C²/N ∙ m²,
k  – współczynnik proporcjonalności (tzw. stała elektrostatyczna) równy 9 ∙ 10⁹ N ∙ m²/C²,
r  – odległość pomiędzy środkami dwóch obiektów.

Zgodnie z prawem Coulomba wartość elektrostatycznego oddziaływania pomiędzy dwoma ciałami jest tym większa, im ciała te są bardziej naładowane (duża wartość ładunku q ) oraz im mniejsza jest dzieląca je odległość (mała wartość r ). Wielkość oddziaływania F  jest tym mniejsza, im większa jest odległość dzieląca dwa ciała oraz im mniejszy jest ładunek tychże ciał. Wykres siły F  od odległości r  pomiędzy dwoma ładunkami znajdziesz w artykule Prawo Coulomba – zadanie nr 4.

Jednostką siły oddziaływania elektrostatycznego jest niuton (N), który zgodnie z powyższym wzorem wyrażony jest przez jednostkę ładunku elektrycznego, który na cześć odkrywcy tego prawa wyrażany jest w kulombach (oznaczenie: C), jednostkę stałej elektrostatycznej (N ∙ m²/C²) oraz jednostkę odległości (m).

Prawo Coulomba – wypadkowa sił działających na ładunek

W oparciu o prawo Coulomba możemy także obliczać wypadkową sił działających na naładowane ciało. Gdy mamy do czynienia z układem n  ciał, naładowanych dodatnio lub ujemnie, to ciała te oddziałują na siebie niezależnie w parach. Wypadkowa wszystkich sił  $\vec{F}_{wyp}$  działających np. na cząstkę 1 jest równa sumie wektorowej sił i wynosi:

$$\vec{F}_{1wyp} = \vec{F}_{12} + \vec{F}_{13} + … + \vec{F}_{1n}$$

gdzie  $\vec{F}_{12}$  to siła elektrostatycznego oddziaływania cząstki 2 na cząstkę 1 itd.

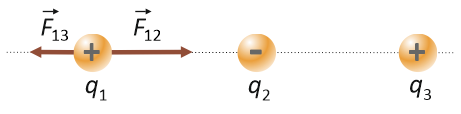
Na przykład, dla układu dodatnich i ujemnych ładunków przedstawionych na powyższym rysunku, wypadkowa siła z jaką ładunek q₂  i q₃  oddziałują na ładunek q₁, wynosi:

$$\vec{F}_{1wyp} = \vec{F}_{12} + \left( \hspace{.05cm} – \hspace{.1cm} \vec{F}_{13} \right) = \vec{F}_{12} \hspace{.15cm} – \hspace{.1cm} \vec{F}_{13}$$