Prawo Coulomba – zadanie nr 4
Dwa punktowe ładunki elektryczne oddalone o 20 cm oddziałują na siebie siłą o wartości 5 N. Sporządź tabelkę wartości sił oddziaływania elektrostatycznego tych ładunków dla odległości od 1 cm do 30 cm z krokiem co 1 cm i przedstaw na wykresie zależność siły F od odległości r pomiędzy ładunkami.
Obliczenie wartości siły oddziaływania elektrostatycznego pomiędzy ładunkami w funkcji odległości będzie wymagało znajomości wartości iloczynu tych dwóch ładunków. W treści zadania podano wartość F dla odległości r równej 20 centymetrów. Przekształcając wyrażenie opisujące oddziaływanie elektrostatyczne pomiędzy naładowanymi elektrycznie ciałami do poniższej postaci (zobacz: prawo Coulomba):
$$F = k \hspace{.05cm} \frac{|q_1| \hspace{.05cm} |q_2|}{r^2} \hspace{1cm} \longrightarrow \hspace{1cm} |q_1| \hspace{.05cm} |q_2| = \frac{F \hspace{.05cm} r^2}{k}$$
będziemy mogli obliczyć wartość iloczynu $|q_1| \hspace{.05cm} |q_2|$. Po podstawieniu wartości liczbowych do powyższego wyrażenia otrzymamy:
$$|q_1| \hspace{.05cm} |q_2| = \frac{5 \hspace{.05cm} \textrm{N} \cdot \left( 0,\hspace{-.1cm}2 \hspace{.05cm} \textrm{m} \right)^2}{9 \cdot 10^9 \hspace{.05cm} \tfrac{\textrm{N} \cdot \textrm{m}^2}{\textrm{C}^2}} = \frac{5 \hspace{.05cm} \textrm{N} \cdot 0,\hspace{-.1cm}04 \hspace{.05cm} \textrm{m}^2}{9 \cdot 10^9 \hspace{.05cm} \tfrac{\textrm{N} \cdot \textrm{m}^2}{\textrm{C}^2}} = \frac{5 \hspace{.05cm} \textrm{N} \cdot 4 \cdot 10^{-2} \hspace{.08cm} \textrm{m}^2 \cdot 10^{-9}}{9 \hspace{.05cm} \tfrac{\textrm{N} \cdot \textrm{m}^2}{\textrm{C}^2}} = 2,\hspace{-.1cm}2 \cdot 10^{-11} \hspace{.05cm} \textrm{C}^2$$
Znając wartość iloczynu ładunków możemy przystąpić do obliczenia wartości siły F w funkcji odległości r dla zakresu odległości podanego w treści zadania. W tym celu możemy skorzystać np. z arkusza kalkulacyjnego.
| Odległość r (m) | Siła F (N) |
|---|---|
| 0,01 | 1980,0 |
| 0,02 | 495,0 |
| 0,03 | 220,0 |
| 0,04 | 123,8 |
| 0,05 | 79,2 |
| 0,06 | 55,0 |
| 0,07 | 40,4 |
| 0,08 | 30,9 |
| 0,09 | 24,4 |
| 0,10 | 19,8 |
| 0,11 | 16,4 |
| 0,12 | 13,8 |
| 0,13 | 11,7 |
| 0,14 | 10,1 |
| 0,15 | 8,8 |
| 0,16 | 7,7 |
| 0,17 | 6,9 |
| 0,18 | 6,1 |
| 0,19 | 5,5 |
| 0,20 | 5,0 |
| 0,21 | 4,5 |
| 0,22 | 4,1 |
| 0,23 | 3,7 |
| 0,24 | 3,4 |
| 0,25 | 3,2 |
| 0,26 | 2,9 |
| 0,27 | 2,7 |
| 0,28 | 2,5 |
| 0,29 | 2,4 |
| 0,30 | 2,2 |
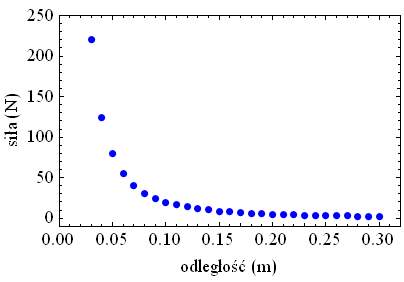
Zwróć uwagę, że wraz ze wzrostem odległości między ładunkami siła oddziaływania elektrostatycznego bardzo szybko maleje. Dla porównania: gdy r wzrasta o rząd wielkości z 0,01 m do 0,1 m wartość F maleje dokładnie o dwa rzędy z 1980,0 N do 19,8 N. Przykład ten dowodzi poprawności wykonanych obliczeń, ponieważ zgodnie z prawem Coulomba siła F jest odwrotnie proporcjonalna do kwadratu odległości r pomiędzy obiektami. Zależność ta, celem lepszego zobrazowania pominięto dwa pierwsze punkty, została przedstawiona na poniższym wykresie:

3 komentarze
osobapróbującasięuczyć
Dodano dnia 25 października 2022 o godz. 21:24
nie wiem jakim cudem z 5 x 0,2^2/9×10^9 moze wyjść 2,2 i jeszcze do tego 10^-11. albo trzeba dokładnie wyjaśnić jak się do tego doszło albo po prostu mnie inaczej matematyki uczyli niż autora tutaj.
Admin
Dodano dnia 27 października 2022 o godz. 11:20
Rozszerzyłem zapis tego równania, żeby nie było już wątpliwości skąd się wziął wynik końcowy.
Bardzo mądry głupi fizyk
Dodano dnia 11 grudnia 2018 o godz. 12:24
Bardzo spoko zadania. Podobają mi się, i mówię tak ogólnie, o wszystkich działach. Więcej takich stron i internet będzie lepszy. 🙂