Natężenie pola elektrycznego – zadanie nr 2

Dwa ładunki q₁ = 1 ⋅ 10^-5 C oraz q₂ = 3 ⋅ 10^-5 C znajdują się w odległości l  = 0,2 m od siebie. Znajdź punkt, w którym natężenie pola elektrycznego jest równe zero.

(Zadanie ze zbioru: K. Chyła Zbiór prostych zadań z fizyki dla uczniów szkół średnich)

Ładunki q₁ i q₂ są ładunkami dodatnimi, w związku z czym wektor natężenia pola elektrycznego będzie zwrócony od tych ładunków. Sytuację tą przedstawia poniższy rysunek:

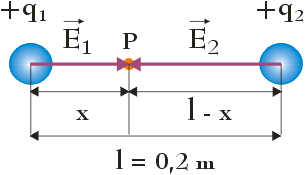
Zauważ, że wektory $\vec{E}_1$  i  $\vec{E}_2$, związane odpowiednio z ładunkiem q₁ i q₂, mają przeciwne zwroty. Punkt P, leżący na linii łączącej obydwa te ładunki, odpowiada punktowi, w którym wypadkowe natężenie pola elektrycznego $\vec{E}_{wyp}$  jest równe zero. Zgodnie z rysunkiem, odległość punktu P od ładunku q₁ wynosi x, z kolei od ładunku q₂: l  – x. Zgodnie z wprowadzonymi oznaczeniami natężenie pola elektrycznego w punkcie P wytworzonego przez każdy z tych ładunków wynosi:

– w przypadku ładunku q₁:

$$E_1 = k \hspace{.05cm} \frac{q_1}{x^2}$$

– w przypadku ładunku q₂:

$$E_2 = k \hspace{.05cm} \frac{q_2}{\left( l \hspace{.1cm} – \hspace{.1cm} x \right)^2}$$

Wiemy, że w punkcie P wypadkowe natężenie pola będącego wypadkową sumą wektorową wektorów $\vec{E}_1$  i  $\vec{E}_2$ wynosi zero, w związku z czym wektory $\vec{E}_1$  i  $\vec{E}_2$ muszą mieć jednakową wartość:

$$E_1 = E_2 \hspace{1cm} \longrightarrow \hspace{1cm} k \hspace{.05cm} \frac{q_1}{x^2} = k \hspace{.05cm} \frac{q_2}{\left( l \hspace{.1cm} – \hspace{.1cm} x \right)^2}$$

Po skróceniu oraz przekształceniu powyższego równania, dostaniemy:

$$\left( \frac{l \hspace{.1cm} – \hspace{.1cm} x}{x} \right)^2 = \left( \frac{l}{x} \hspace{.1cm} – \hspace{.1cm} 1 \right)^2 = \frac{q_2}{q_1}$$

skąd po spierwiastkowaniu, otrzymamy:

$$\frac{l}{x} \hspace{.1cm} – \hspace{.1cm} 1 = \sqrt{\frac{\mathstrut q_2}{q_1}} \hspace{1cm} \longrightarrow \hspace{1cm} \frac{l}{x} = \sqrt{\frac{\mathstrut q_2}{q_1}} + 1$$

i w efekcie:

$$x = \frac{l}{\sqrt{\dfrac{\mathstrut q_2}{q_1}} + 1}$$

Po podstawieniu do powyższego równania wartości liczbowych podanych w treści zadania oraz wykonaniu obliczeń, dostaniemy szukaną odległość punktu P od ładunku q₁, równą:

$$x = \frac{0,\hspace{-.1cm}2 \hspace{.05cm} \textrm{m}}{\sqrt{\dfrac{\mathstrut 3 \cdot 10^{-5} \hspace{.05cm} \textrm{C}}{1 \cdot 10^{-5} \hspace{.05cm} \textrm{C}}} + 1} = 7,\hspace{-.1cm}3 \hspace{.05cm} \textrm{cm}$$